Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Probabilité : Conditionnement - IndépendanceTopics traitant de Probabilité : Conditionnement - Indépendance [tout]Lister tous les topics de mathématiques
Niveau terminale
probabilité
Posté par khmc9
Bonjour,
je bloque sur un exercice de probabilité voici le sujet :
Citation :
on a mené une étude sur les candidats se présentant au bac. 96% des candidats révisent avant de passer l'épreuve. Par ailleurs, un candidats ayant réviser a tout de même une chance sur dix de ne pas obtenir son bac et parmis les candidats n'ayants pas révisé 95% seulement sont recalés. On rencontre au hasard un candidats après les résultats de l'examen. On considère les événements : A " le candidat est admis " et R " le candidats a révisé "
on a mené une étude sur les candidats se présentant au bac. 96% des candidats révisent avant de passer l'épreuve. Par ailleurs, un candidats ayant réviser a tout de même une chance sur dix de ne pas obtenir son bac et parmis les candidats n'ayants pas révisé 95% seulement sont recalés. On rencontre au hasard un candidats après les résultats de l'examen. On considère les événements : A " le candidat est admis " et R " le candidats a révisé "
1) Construire un arbre pondéré décrivant la situation :
j'ai fais cela :
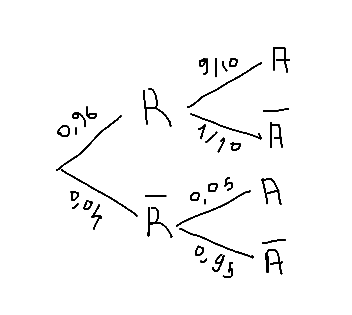
2) Calculer les probabilité qu'un candidat : soit admis et ait révisé , soit admis , soit admis ou ait révisé :
P(A
 R) = 0,864
R) = 0,864
P(A) = P(a
 R) + P ((1-R)
R) + P ((1-R) A) = 0,866
A) = 0,866
P(A
 R) = P(A)+P(R)-P(A
R) = P(A)+P(R)-P(A R) = 0,962
R) = 0,962
3 ) On interroge un candidats ayant révisé. Quelle est la probabilité qu'il ait obtenu son bac ?
Pr(A) = 0,9
4) calculer Pa(R)
Pa(R) = 0,99
5 ) Le jour des résultats tous les recus font les malins en prétendant qu'ils n'ont pas eu besoin de réviser et tous les recalés crient a l'injustice en affirmant avoir travaillé jour et nuit.
Expliquer clairement pourquoi la probabilité qu'un candidat soit un menteur est égale a 0,902
je n'arrive pas a répondre a cette question ...
Donc tout le monde ?
Relis bien l'énoncé de la question 5.
TRu dois y trouver 2 catégories de menteurs.
khmc9 @ 01-01-2017 à 19:16
les menteurs sont ceux qui disent avoir ou ne pas avoir révisé ?
les menteurs sont ceux qui disent avoir ou ne pas avoir révisé ?
il y a une première catégorie de menteur : ceux qui après l'obtention de leur bac disent ne pas avoir révisé => Pa((1-R))
et la deuxieme catégorie de menteur sont ceux qui après ne pas avoir eu leur bac se plaigne d'avoir révisé => P1-a(R)
Non.
Ce sont :
Ceux qui ont révisé et obtenu leur bac (car "tous les recus font les malins en prétendant qu'ils n'ont pas eu besoin de réviser ") , et ... ?
Yzz @ 01-01-2017 à 19:39
Non.
Ce sont :
Ceux qui ont révisé et obtenu leur bac (car "tous les recus font les malins en prétendant qu'ils n'ont pas eu besoin de réviser ") , et ... ?
Non.
Ce sont :
Ceux qui ont révisé et obtenu leur bac (car "tous les recus font les malins en prétendant qu'ils n'ont pas eu besoin de réviser ") , et ... ?
Donc c'est P( A
 R) =0,864
R) =0,864
et ceux qui ont pas révisé et pas eu leur bac : P ( (1-A)
 ( 1-R))=1-p(A
( 1-R))=1-p(A R)
R) 

