Inscription / Connexion Nouveau Sujet
Probabilité
Une salle de spectacle, propose pour la saison, des abonnements pour 4,5 ou 6 spectacles.
Dans la population des abonnés, la répartition est la suivante:
- 43,5 % ont choisi l'abonnement 4 spectacles,
- 33 % ont choisi l'abonnement 5 spectacles,
- le reste a choisi l'abonnement 6 spectacles.
On interroge deux abonnés au hasard. On admet que le nombre d'abonnés est suffisamment grand pour assimiler le choix de deux abonnés à des tirages successifs indépendants avec remise.
On note A l'évènement "l'abonné interrogé a choisi 4 spectacles" ; B l'évènement " l'abonné a choisi 5 spectacles" ; c l'évènement "l'abonné a choisi 6 spectacles".
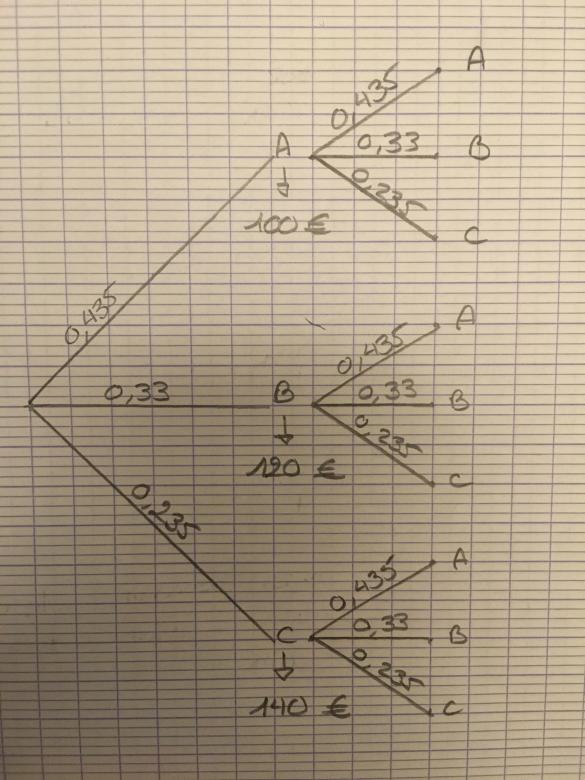
1) Modéliser à l'aide d'un arbre pondéré cette situation.
2) L'abonnement pour 4 spectacles coûte 50 euros, celui pour 5 spectacles coûte 60 euros , et celui pour 6 spectacles coûte 70 euros. On appelle X la variable aléatoire égale à la somme totale dépensée par les deux abonnés interrogés.
a) Déterminer la loi de probabilité complète de X (organiser la réponse sous forme de tableau ; les probabilités seront arrondies à 10 -3près).
b) Calculer l'espérance de x. Interpréter.
Voici donc l'énoncé. Concernant cet exercice, je n'arrive pas a faire la 2) a) et b) . D'autre part, je pense que j'ai réussi l'arbre pondéré. J'ai fait 3 branches car il y a 3 événements et et sur chacune de ces branches, j'ai refait 3 branches.
Merci de votre aide.
(Bonjour?)
C'est de l'application directe du cours, voir partie 2 grand b https://www.kartable.fr/premiere-s/mathematiques/specifique/chapitres-177/les-probabilites-16/cours/les-probabilites-4/4073 ( je n'ai pas trouvé le cours sur ilemaths )
euh non, pas vraiment, relis ton énoncé
X vaut la somme dépensée par les deux abonnés, pas par un seul
mets au bout de chaque branche de ton arbre la somme dépensée par les deux personnes
et marque les proba sur chaque branche
avec ça, tu sauras ensuite répondre aux questions
Merci beaucoup malou. J'ai compris mais un petit détail, combien de fois dois-je refaire les branches ?? 2 fois ??
non...
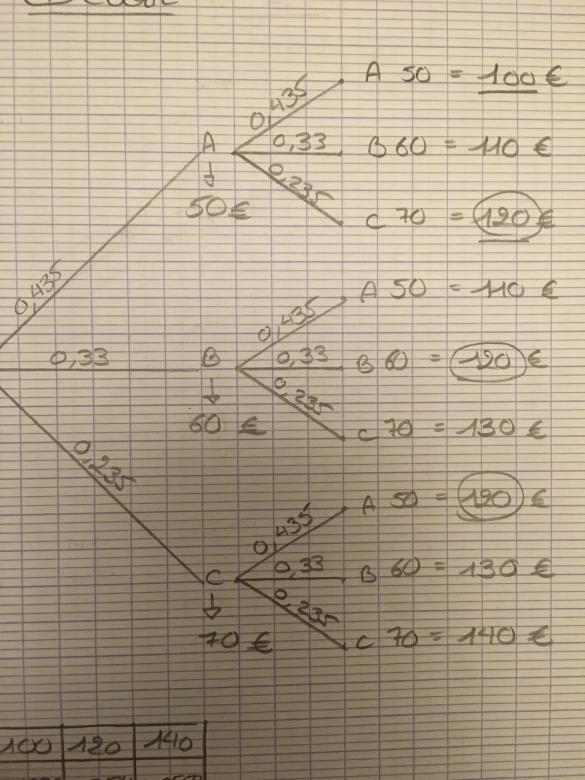
remplace ton 100 par 50 ; ton 120 par 60 et ton 140 par 70
cela concerne la personne n°1
et au bout des autres branches, tu fais pareil, 50 ; 60 et 70 pour la 2e personne
et ensuite tu vas pouvoir faire les sommes "au bout du bout "de chaque branche
| x1 | 100 | 120 | 140 |
| p(X=x1) | 0,1892 | 0,3134 | 0,0552 |
voici le tableau sauf que les valeurs de la deuxième ligne ne sont pas égales a 1, pourquoi ?
parce qu'il te manque plein de possibilités...
ton arbre (comme je préconisais au dessus) est certainement faux...
Voici mon interprétation: si on répète un très grand nombre de fois l'expérience, la somme totale dépensée par les deux abonnés interrogés sera en moyenne de 116€.
Est-ce bon ?