Bonjour,

Ton arbre est vraiment difficile à lire ... Si j'ai bien compris, tu as voulu écrire un arbre comme ceci :

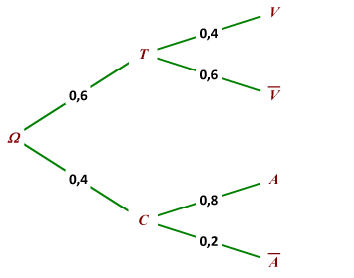
Dans ce cas, avec les notations que tu donnes, il correspond bien à l'énoncé.

Pour la question 2, il s'agit sans doute d'une loi binomiale. Mais ton énocé est incomplet.

Bonjour, je vous remercie pour votre réponse et effectivement cela correspond bien à cela mais je ne trouvais pas comment faire l'arbre de probabilité ....

Pour la question numéro 2A, j'ai effectivement oublié quelques choses : Ils nous disent qu'ils interrogent 30 clients à la sortie du magasin, indépendamment les uns des autres

Soit X la variable aléatoire égale au nombre de clients ayant acheté du thé vert;

2.B j'ai réussi à la faire

2.C
LE CA réalisé pour la vente d'un sachet de 100g de thé vert est de 8,50
Calculer son espérance, j'ai réussi à le faire mais par la suite ils demandent : Quel CA l'entreprise peut espérer réaliser en moyenne pour 30 clients sur le vente de thé verts

Merci beaucoup

Question 2A)
L'expérience aléatoire est une répétition de 30 épreuves indépendantes à 2 issues :
-> le client a acheté du thé vert (succès)
-> le client n'a pas acheté du thé vert (échec)
On reconnaît bien un schéma de Bernoulli qui conduit à une loi binomiale. Il s'agit d'en préciser les paramètres.

Je vous remercie monsieur,

J'ai des difficultés en mathématiques, et préciser les paramètres cela correspond bien à p et n cependant comment les trouver ?

A quoi correspondent-ils ?

Cordialement

n est le nombre de répétitions de l'épreuve à 2 issues : n=30
p est la probabilité d'avoir un succès. Ici p=P_T(V) (voir l'arbre pondéré).

Pardon, je me suis trompé. La probabilité d'un succès est p=p(TV)=p(T)p_T(V).

Je vous remercie de l'aide que vous me fournissez monsieur,

Il y a une question plus haut avec l'arbre pondéré mais je ne suis pas sûr de la réponse,
La question est : Quel est la probabilité que le client ait acheté du thé vert ou du café arabica

J'ai mis : P (V ou A)= P(V)+(A)-P(V et A)= 0,86

Ensuite ils demandent : calculer la probabilité que le client n'ai acheté ni thé vert ni café arabica

J'ai mis : 1-P(V ou A)=1-0,86= 0,14

Est-ce bon ?

Cordialement

L'évènement  (V ou A) est la réunion de 2 évènements incompatibles : ils ne peuvent pas se produire en même temps car un client qui achète un produit ne peut pas avoir en même temps du thé vert et du café arabica.
Donc p(VA)=p(V)+p(A)-p(VA) avec p(VA)=0.
Donc p(VA)=p(V)+p(A). Je ne trouve pas 0,86 ...

P(V)+P(A)=1,2 ce n'est pas possible ...

Tu fais erreur. Dans l'arbre pondéré, pour obtenir p(V) il faut multiplier les probabilité qui sont sur les branches menant à l'évènement V... Même chode pour l'évènement A.

Ainsi : p(V)  =  p(T)p_T(V)  =  0,60,4

Deux fautes dans la même phrase : "il faut multiplier les probabilités" et "Même chose..."
Voila ce qui arrive quand on ne prend pas le temps de se relire

Pour l'événement A cela fait :
P(C) x Pc(A)=0,32

Donc P(A)+P(B)=0,32+0,24=0,56

Donc la question qui suit, quel est la probabilité que les client n'achètent ni du thé vert ni du café arabica c'est égal à 1-0,56=0,44 ?

Merci

Oui, c'est ça

Je vous remercie, mais j'aimerais être sur de ces probabilités :

P(T)=0,6
P t(V)=0,4
Pc(A)=0,8

Merci

Désolé, je me suis absenté quelques temps ...

C'est tout juste.

Bonjour,

Je vous remercie pour votre aide  et j'aimerais vous demander votre avis sur ce calcul :LE CA réalisé pour la vente d'un sachet de 100g de thé vert est de 8,50
Calculer son espérance, quel CA l'entreprise peut espérer réaliser en moyenne pour 30 clients sur le vente de thé verts :

E(X)=n*p=30*0,24=7,20

Cependant le reste je n'y arrive pas que faut-il faire ?

Merci

L'espérance est correcte. Elle signifie qu'en moyenne, lorsque 30 clients passent dans le magasin pour acheter un produit, le commerçant va faire un chiffre d'affaires de 7,20 euros sur le thé vert. Tout simplement.

Bonsoir,
j'ai comme un doute.

Si, en moyenne sur 30 clients, 7,2 achètent du thé vert à 8,50€ il me semble que le chiffre d'affaire généré par le thé vert est 7,28,50 en euro.

Bonsoir verdurin

Oui, tu as raison. La variable X donne le nombre de clients ayant acheté du thé vert parmi les 30 clients.... Donc le chiffre d'affaires généré par le thé vert est bien celui que tu donnes

J'ai répondu trop vite sans relire l'énoncé...

Remarque que j'ai écrit « le chiffre d'affaire » au lieu de « l'espérance du chiffre d'affaire ».
C'est difficile de répondre sans aller trop vite.

Je vous remercie énormément de votre aide.

On interroge n clients, au hasard et indépendamment les uns des autres

4.Calculer la probabilité qu'aucun client n'ait acheté du thé vert et déduire l'écriture de probabilité qu'au moins un client ait acheté du thé vert.

Voici ce que j'ai fait.

B(n;0,24)

Et l'écriture de probabilité:

P(X>1)

5. Que signifie cette ligne tiré d'un algorithme

TANT QUE_(1-pow(0.76,n)<0,9999) FAIRE

J'ai mis que tant que la probabilité qu'aucun client n'ai acheté du thé vert soit inférieur à 0,99999 il faut refaire l'expérience

6. Montrer que résoudre 1-0,76^n=0,999 est la même chose que n*ln(0,76)=0,001
et déterminer n un entier naturel
1-0,76^n=0,999
-0,76^n+1=0,999
-0,76^n=-0,001
0,76^n=0,001
log(0,76^n)=log(0,001)
n*(log(0,76))=log(0,001)
n=log(0,001)/log(0,76)
n=25,17

ln(0,76)=0,001
n=0,001/ln(0,76)
n=-0,0036

Je ne sais pas comment prouver que les 2 équations sont équivalentes mais en plus la valeur de n selon mes calculs ne sont pas les mêmes dans les 2 équations ...

Merci beaucoup

    

Pour la question 4, il est plus simple de calculer la probabilité de l'évènement contraire. L'évènement contraire de "X > 1"  est "X = 0" (dans ce cas particulier).

Pour la question 5, la ligne que tu donnes n'est pas tirée d'un algorithme car elle n'est pas constituée de mots français. Elle contient un mot (pow) appartenant au vocabulaire d'un langage de programmation (Algobox par exemple). Elle aurait dû s'écrire : Tant que (1-n^0,76) < 0,9999. Une fois de plus on mélange algorithme et programme.
Ta conclusion n'est sans doute pas celle qui est attendue. Il faut comprendre que 0,9999 est très proche de 1. Donc si c'est la probabilité d'un évènement, c'est l'évènement "presque" certain...

Pour la question 6, il y a sans doute une erreur sur la question posée. La question aurait dû être :
"Montrer que résoudre 1-0,76ⁿ=0,999 est la même chose que nln(0,76)=ln(0,001)"... ce que tu as fait d'ailleurs. L'entier à trouver est 25 ou 26 mais certainement pas 25,17

Je vous remercie monsieur pour toute l'aide que vous me donner afin de comprendre cet exercice, j'aimerais savoir pourquoi dans ce cas précis l'événement contraire de P(X>1) est P(X=0) ?

Pour la question 6, la question que j'ai écrire est la bonne ... Y a t-il une erreur dans le sujet ?

En ayant trouver n=25 il est demandé de déduire le nombre de clients qu'il faut interroger à la sortie du magasin pour que la probabilité d'obtenir au moins un client ayant acheté du thé vert soit supérieur à 0,999.

Faut il utiliser la loi binomiale ?

Cordialement.

"P(X>1)" n'est pas un évènement mais une probabilité, donc un nombre.
Dans une loi binomiale, de paramètres n et p, la variable X est un entier qui varie de 0 à n inclus.
Donc l'évènement "X>1" contient les évènements {"X=2", "X=3", "X=4", ..., "X=n"}

Donc, et je me suis effectivement trompé, l'évènement contraire de "X>1" est l'évènement "X=0" ou "X=1". Il n'empêche  : il est plus simple de calculer p(X>1) en utilisant la probabilité de l'évènement contraire :
p(X>1) = 1 - p(X=0) - p(X=1).

Cependant, j'ai été induit en erreur par la question 4 : "Calculer la probabilité qu'aucun client n'ait acheté du thé vert et déduire l'écriture de probabilité qu'au moins un client ait acheté du thé vert." autrement dit : "Calculer p(X=0) et en déduire p(X1)".

Tu as démontré à cette question 4 que p(X=0) = 0,76ⁿ.

Tu en as déduit que p(X1) = 1 - p(X=0) = 1 - 0,76ⁿ

Ensuite, à la question 6, tu devais démontrer que résoudre 1-0,76ⁿ=0,999 équivaut à résoudre n ln(0,76) = ln(0,001) (je persiste à dire qu'il y a une erreur dans ton énoncé ici).

Tu peux en déduire : p(X) > 0,999 1-p(X=0) > 0,999
ou encore :  p(X) > 0,999 1-p(X=0) > 1-0,001
ou encore :  p(X) > 0,999 -p(X=0) > -0,001
ou encore :  p(X) > 0,999 p(X=0) < 0,001  (l'inégalité change de sens car on multiplie par -1)
ou encore :  p(X) > 0,999 0,76ⁿ < 0,001
ou encore :  p(X) > 0,999 n ln(0,76) < ln(0,001)
ou encore :  p(X) > 0,999   (l'inégalité change encore de sens car on divise par le nombre ln(0,76 qui est négatif)

Donc, n étant un entier tel que n>25,17..., on peut dire qu'il faut interroger au moins 26 clients pour que la probabilité d'obtenir au moins un client ayant acheté du thé vert soit supérieure à 0,999.

Petit oubli dans la ligne "Tu peux en déduire ...".

Il fallait lire "Tu peux en déduire : p(X1) > 0,999 1-p(X=0) > 0,999

Toutes les lignes suivantes ont le même oubli car j'ai fait du copier-coller ...

Je vous remercie pour toutes vos aides.

La question 4, j'ai oublié un élément dans la question ... C'est : Calculer en fonction de n, la probabilité qu'aucun client n'ait acheté du thé vert

C'est donc bien : p(X=0) qu'il faut calculer ?

Ensuite l'écriture de probabilité qu'au moins qu'un client ait acheté du thé vert
P(X > ou égal à 1)

C'est bien cela ?

Cordialement

Bonjour,

effectivement je ne l'ai pas compris ... Moi et les maths c'est difficile, dans la question il est écrit en fonction de n je m'attendais à voir un "n" quelque part ...

Mais il est bien présent le n :

p(X=0)=0,76ⁿ

salut

l'enoncé est tres mal construit ou recopié  :

C'est vrai que j'avais vu l'erreur mais je ne suis pas surpris : le pronom relatif dont ne fait hélas plus partie du vocabulaire courant de nos lycéens