A un carrefour juge dangereux, la gendarmerie décide d'effectuer un contrôle de façon aléatoire chaque jour. Pour n un entier naturel non nul, on note:
Cn l'évènement: la gendarmerie décide d'effectuer un contrôle le n eme jours à ce carrefour
Cn(barre) L'événement contraire de Cn
1) Des contrôles indépendants
Soit p un réel fixé dans l'intervalle [0;1]
Dans cette question uniquement on suppose que
La probabilité que la gendarmerie décide d'effectuer un contrôle un jour donné est égale à p
Le choix de faire un contrôle ou pas est indépendant d'un jour à l'autre
La probabilité que la gendarmerie effectué exactement un contrôle deux jours consécutifs et d'au moins 0,455
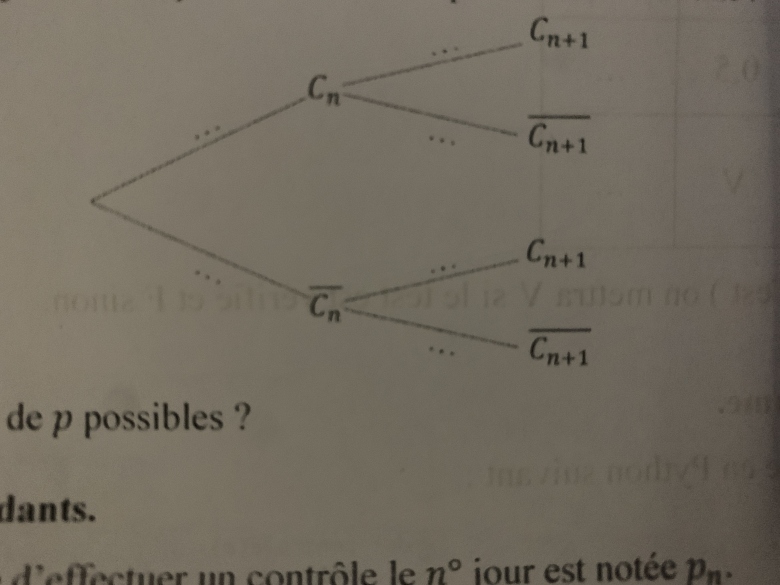
a) reproduire sur votre copie et compléter l'arbre de probabilité suivant
b) quelles sont les valeurs de p possibles?
2) Des contrôles nom indépendants
La probabilité que la gendarmerie des sites effectuer un contrôle le n eme jour est noté Pn
On suppose maintenant que
Le premier jour la gendarmerie décide de faire un contrôle à ce carrefour
Si un jour donné la gendarmerie a décidé d'effectuer un contrôle à ce carrefour alors la probabilité qu'elle décide d'effectuer un contrôle le jour suivant est de 0,35
Si un jour donné la gendarmerie a décidé de ne pas effectuer un contrôle à ce carrefour alors la probabilité qu'elle décide d'effectuer un contrôle le jour suivant est de 0,65
à) que Val P1 et P2 d'après l'énoncé?
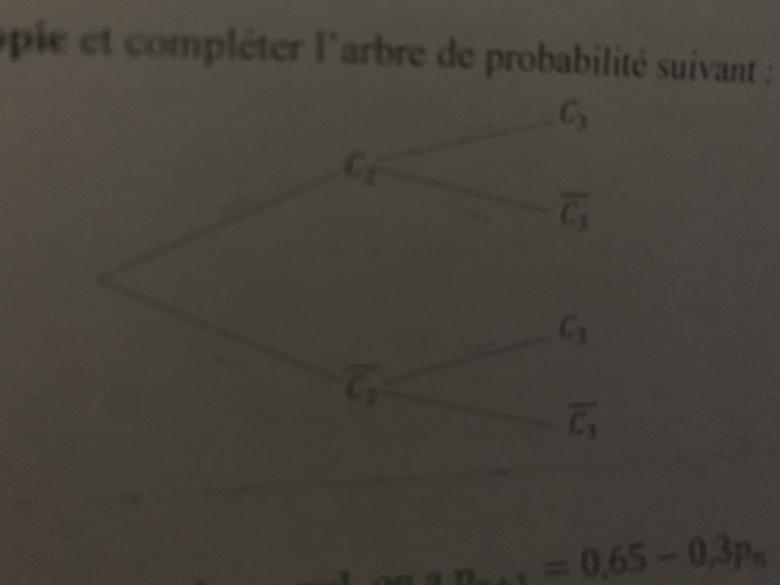
b) reproduire ça va te copier et compléter l'arbre de probabilité suivant
c) calculer P3
d) montrer que pour tout entier naturel non nul on a Pn+1= 0,65 -0,3pn
e) en déduire la probabilité que la gendarmerie décide de faire un contrôle à ce jour le cinquième jour.