Inscription / Connexion Nouveau Sujet
probabilité
Bonjour,
Pouvez-vous m'aider à cette exercice qui est à rendre bientôt s'il vous plaît je n'arrive vraiment pas pas.
On donne le paramétrage d'une machine à sous dans un casino:
Si elle donne un gain lors d'une utilisation, la probabilité qu'elle en donne un à l'utilisation suivante est 0,01.
Si elle ne donne pas de gain, la probabilité qu'elle en donne un à l'utilisation suivante est 0,1.
Pour tout entier naturel non nul, on note Gn l'événement "la n-ième utilisation donne un gain" et on note pn la probabilité de cet événement.
Pour la première partie, la probabilité d'obtenir un gain est 0,2, on a donc p1= 0,2.
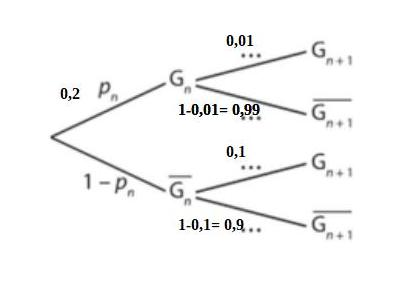
1. Recopier et compléter l'arbre ci-contre en y inscrivant les bonnes probabilités.
2. Montrer que, pour tout entier naturel n non nul, Pn+1= -0,09Pn + 0,1
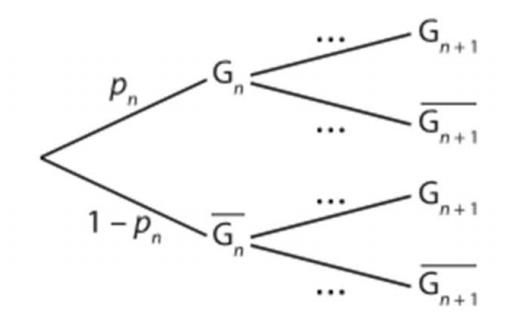
c'est exact, note cette proba sur la bonne branche
1) l'énoncé précise que p1 = 0.2
donc sur la branche primaire, on note 0.2 (à la place de pn)
et tu peux ainsi pondérer toutes les branches de l'arbre.
que trouves-tu ?
parfait
reste à calculer 1- p1 et à mettre cette proba sur l'arbre
2. Montrer que, pour tout entier naturel n non nul, Pn+1= -0,09Pn + 0,1
tu dois utiliser la formule des probabilités totales, tu essaies ?
Il faut calculer à l'aide de la formule de la formule des probabilités totale en laissant pn et 1-pn ?
non, dans cette première partie, tu utilises l'arbre que tu viens de compléter,
on est toujours sur ce cas particulier de n=1