Inscription / Connexion Nouveau Sujet
Probabilité
Bonjour! J'ai un autre exercice,j'ai besoin de savoir si c'est correct.
Dans un garage,il y a exactement 21 voitures en réparation pour freins ou changement d'huile du moteur.parmi les 11 voitures destinées à être réparées en freins,il y en a 6 pour changement d'huile.Boss Alfred commence sa journée de travail en choisissant au hasard l'une de ces voitures.La probabilité de choisir une voiture seulement pour changement d'huile est...
Données:
n=21voitures
Parmi 11voitures(5 destinées à être réparées en freins et le reste(5 pour changement d'huile du moteur.
P=1 et à la fin,il nous reste 10 voitures destinées à être réparées à la fois en freins et pour changement d'huile du moteur.
Solution
Soit A l'évenement la probabilité de choisir une voiture pour changement d'huile seulement est:
P(A)=cardA/cardΩ
P(A)=6C1×5C0×10C0/21C1
P(A)=6×1×1/21
P(A)=6/21=>[P(A)=0,28] est ce que c'est correct? Merci d'avance pour votre aide.

Bonsoir
Parmi les 11 voitures destinées à être réparées en freins, il y en a 6 pour le changement d'huile.
Bonjour!Je ne comprends pas trop,je veux plus d'explication.est ce que c' est correct OU pas?
Bonjour
On dit j'aimerais où je souhaiterais....
Merci d'en tenir compte

bonjour,
en attendant le retour de hekla :
tu devrais remplir le tableau que hekla t'a donné : tu y verras les effectifs qui correspondent à card(A), très clairement.
sinon tu peux te dire aussi que "huile seule" c'est aussi "pas les freins".... 
as tu rempli le tableau ?
quel effectif as tu trouvé dans la case huile seule (huile, pas le freins) ?
Bonjour! Oui j'ai essayé mais ce n'est très Claire pour moi.j'ai beaucoup réfléchi la dessus en fin j'ai failli abandonner mais quand même je rempli le tableau.je ne le rempli pas complètement mais j'ai fait de mon mieux même si je ne suis pas sûr de ce que j'ai fait. Voici le tableau.
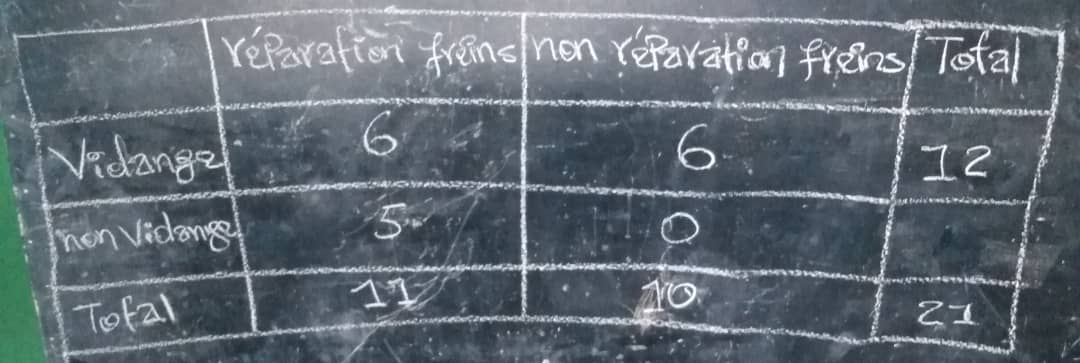
Là, on est bien d'accord. Combien de véhicules dans la case vidange sans réparation de freins, ce que vous avez appelé comme événement A ?
D'où la probabilité ?
Oui! D'accord,il y a 10 voitures dans la case vidange sans la réparation de freins.
Donc, on peut dire:
P(A)=10/21=>[P(A)=0,47] n'est ce pas?
D'accord pour
à une nuance près pour 0,47 le chiffre d'après est un 6, l'arrondi aurait dû être 0,48 et
comme ce n'est qu'une approximation, ce n'est pas le signe = mais
Bonjour! d'accord,10/21=0,476≈0,48
à la fin on a [P(A)=0,48].Merci beaucoup tu m'a fait résoudre l'exercice donc merci pour votre patience.



