Inscription / Connexion Nouveau Sujet
Probabilité avec deux urnes
Bonjour ! J'ai un exercice de probabilité à rendre, il est assez long, mais il ne me reste que la dernière question à faire, sur laquelle j'ai un peu de mal.
On dispose de deux urnes U1 et U2 contenant des boules indiscernables au toucher.
U1 contient 12 boules blanches et 3 boules noires, U2 contient 2 boules blanches et une boule noire.
On tire au hasard une boule dans U1 et on la place dans U2. On tire ensuite au hasard, une boule dans U2. L'ensemble de ces opérations constitue une épreuve.
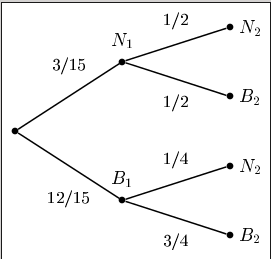
On note B1(respectivement N1) l'évènement "on a tiré une boule blanche (resp. noire) dans l'urne U1".
On note B2(respectivement N2) l'évènement "on a tiré une boule blanche (resp. noire) dans l'urne U2".
Un joueur participe 5 fois de suite à ce jeu, en remettant à chaque fois les boules tirées à leur place. Ce qui fait qu'au début de chaque épreuve, l'urne U1 contient 12 boules blanches et 3 noires, et l'urne U2 contient 2 boules blanches et une oire.
Ainsi les épreuves successives sont indépendantes.
Déterminer la probabilité que ce joueur réalise au moins une fosi l'évènement B2 au coours de ces cinq épreuves (on donnera le résultat sous forme de fraction irréductible puis décimale.)
Voilà, c'est la dernière question.
Je ne suis pas sûre que c'est nécessaire mais dans les questions précédentes, j'ai trouvé p(B2)= 0.7.
Je vous remercie d'avance de votre aide.
J'ai précédemment calculé cette probabilité grâce aux questions d'avant que je n'ai pas postées, étant donné que je les aies réussies.
Mais concrètement c'est avec la formule des probabilités totales que j'ai trouvé B2.
ok
on te dit qu'un joueur répète 5 fois de suite ce jeu, à l'issue de chaque jeu tu as deux issues indépendantes possibles la boule tirée au deuxième tirage est blanche ou la boule tirée au deuxième tirage n'est pas blanche. Cela te fait-il penser à une loi de probabilités particulière ?
En fait jusqu'à maintenant j'ai essayé de considérer le contraire, c'est à dire l'évènement E "Sur les 5 parties on ne tire aucune boule blanche dans l'urne U2".
Soit Ak "On tire une boule blanche à la kième partie".
Je disais ensuite que p(E)=1-p(A1bar A2bar
A2bar A3bar
A3bar A4bar
A4bar A5bar)
A5bar)
Les évènements sont indépendants donc :
p(E)= 1-p(A1bar)*p(A2bar)*p(A3bar)*p(A4bar)*p(A5bar)
J'en suis là mais je ne vois pas comment trouver p(A1bar) etc..
considérer l'événement contraire est une bonne idée, par contre j'attendais que tu me cites une loi de probabilité discrète à savoir une loi binomiale puisque nous sommes en présence d'une répétition de 5 épreuves de Bernoulli. A partir de là tu connais les deux paramètres de la loi Binomiale et tu peux déterminer
P(X 1)=1-P(X=0).
1)=1-P(X=0).
Je ne les ai pas encore étudiées à vrai dire, c'est pour cela que je ne peux pas le faire ainsi, je suis contrainte de passer par l'évènement contraire.
bon tu sais que la probabilité d'avoir une boule blanche au deuxième tirage est de 0,7 donc ne pas en avoir une c'est 1-0.7=0.3
tu veux en faisant 5 fois la même épreuve à chaque fois une boule noire au deuxième tirage. Comment peux-tu traduire cela en terme de probabilités ?
un petit effort de rédaction ? 
X est une variable aléatoire qui désigne, lors de 5 épreuves, le nombre de fois où on a obtenu une boule blanche au deuxième tirage ; on cherche la probabilité d'avoir X  1 donc P(X
1 donc P(X 1)=1-P(X=0).Donc P(X
1)=1-P(X=0).Donc P(X 1)=1-(0.3)5
1)=1-(0.3)5
Oui voilà désolée de la rédaction inexistante ! N'y a-t-il pas une autre manière de noter en utilisant N2=0.3 ?
pourquoi tu n'aimes pas ma rédaction ?
Tu peux dire que P(X=0)=P(N2 N2
N2 N2
N2 N2
N2 N2)comme les évènements sont indépendants P(X=0)=P(N2)
N2)comme les évènements sont indépendants P(X=0)=P(N2) P(N2)
P(N2) P(N2)
P(N2) P(N2)
P(N2) P(N2)=0.35
P(N2)=0.35
Bonjour,
je voulais savoir comment on pouvait faire pour montrer que p(B2)=0.7,
ou plutôt le calcul précédent qui consiste à démontrer que :
p(B2)=(3k+6)/(4K+12)=(3/4)*[(k+2)/(k+3)]
,car je ne comprends pas le chemin pour y parvenir malgré le conseil de Ted sur l'usage de la formule des probabilités totales.
( En effet, dans la suite de l'exercice, on suppose que k=12, d'où, p(B2)=0.7 )
Veuillez m'excuser, j'ai trouver la solution, merci Ted :
p(B2)
= p(B1 ∩ B2)+p(N1 ∩ B2) = p(B1)×pB1(B2)+p(N1)×pN1(B2)
=3k + 6
4k + 12


 B1
B1
