Inscription / Connexion Nouveau Sujet
Probabilité conditionnelle
Bonjour voici un exercice de mathématiques complémentaires sur lequel je souhaiterais avoir de l'aide. Pouvez-vous m'aider?🤗
Énoncé - Questions - réponses - 1 pièce jointe
.
.
.
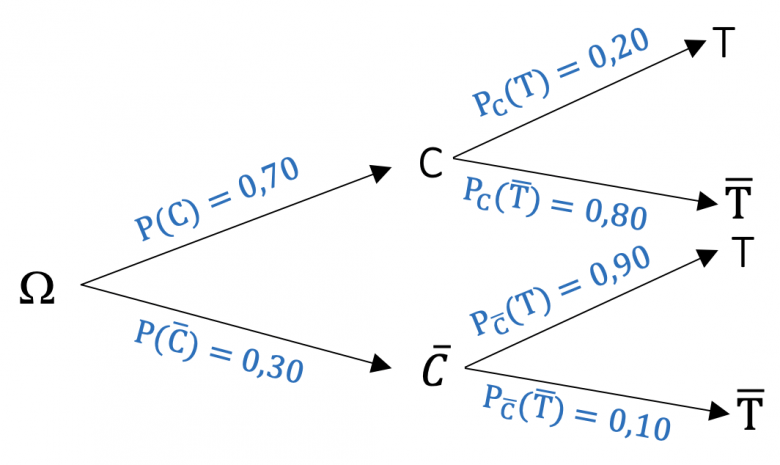
Un propriétaire d'une salle louant des terrains de squash s'interroge sur le taux d'occupation de ses terrains. Sachant que la location d'un terrain dure une heure, il a classé les heures en deux catégories : les heures pleines (soir et week-end) et le heures creuses (le reste de la semaines). Dans le cadre de cette répartition, 70% des heures sont creuses.
Une étude statistique sur une semaines lui a permis de s'apercevoir que :
-> Lorsque l'heure est creuse, 20% des terrains sont occupées;
-> Lorsque l'heure est pleine, 90% des terrains sont occupées.
On choisit un terrain de la salle au hasard. On notera les évènements : C "l'heure est creuse" et T "le terrain est occupée"
1. Représenter cette situation par un arbre de probabilités.
---> Réponse en pièce jointe :
2. Déterminer la probabilité que le terrain soit occupé et que l'heure soit creuse.
--->
3. Déterminer la probabilité que le terrain soit occupé.
---> On cherche P(T)
D'après la loi des probabilités totales, C et forment une partition de l'univers
Soit
4. Montrer que la probabilité que l'heure soit pleine, sachant que le terrains soit occupé, est égal à 27/41.
---> ?
Dans le but d'inciter ses clients, à venir hors des heures de grandes fréquentation, le propriétaire a instauré, pour la location d'un terrain, des tarifs différenciés :
-> 10€ pour une heure pleine;
-> 6€ pour une heure creuse.
On note x la variable aléatoire qui prend pour valeur la recette en euros obtenue grâce à la location d'un terrain de la salle, choisis au hasard, Ainsi X prend 3 valeurs:
-> 10 lorsque le terrain est occupé et loué en heure pleine;
-> 6 lorsque le terrain est occupé et loué en heure creuse;
-> 0 lorsque le terrain n'est pas occupé.
5. Construire un tableau décrivant la loi de de probabilité de X
| Issues de xi | 0 | 6 | 10 |
| P(X = xi) | p1=? | p2=? | p3=? |
6. Déterminer l'espérance de X.
---> E(X) = p1*0 + p2*6 + p3*10 =
7. La salle comporte 10 terrains et est ouverte 70 heures pas semaine. Calculer la recette hebdomadaire moyenne de la salle.
---> Si on répète un grand nombre de fois cette semaine, la recette hebdomadaire est d'en moyenne E(X)€.
.
.
.
Merci d'avance🤗
Bonjour,
Ok pour tes réponses ,et arbre très clair
4)Montrer que la probabilité que l'heure soit pleine, sachant que le terrain soit occupé, est égal à 27/41.
Quelle est la probabilité ?
Quelle est la probabilité P(T)?
5)relis
Ainsi X prend 3 valeurs:
-> 10 lorsque le terrain est occupé et loué en heure pleine;
-> 6 lorsque le terrain est occupé et loué en heure creuse;
-> 0 lorsque le terrain n'est pas occupé.
et regarde ton arbre...
complète en français la probabilité p0est la probabilité que le terrain ......., puisque x0=0
sers toi de l'arbre pour trouver p0 ou de la réponse à la question 1...
La probabilité
La probabilité P(T)= 0,41
La probabilité p0 est la probabilité que le terrain ne soit pas occupé, puisque x0=0
Donc p0= 0,80 + 0,10 = 0,90
.
Est-ce correcte?
oups un oubli de parenthèses.... pour la question 4
4)Montrer que la probabilité que l'heure soit pleine, sachant que le terrain soit occupé, est égal à 27/41.
Quelle est la probabilité ?
Quelle est la probabilité P(T)?
La probabilité P(T)= 0,41 OK
tu peux conclure
5)
La probabilité p0 est la probabilité que le terrain ne soit pas occupé, puisque x0=0 correct
Donc p0= 0,80 + 0,10 = 0,90 faux
relis ta réponse pour la question 3)
= 0,27 et P(T)= 0,41
Alors
5)La probabilité p0 est la probabilité que le terrain ne soit pas occupé, puisque x0=0
Alors p0= 1-0,41= 0,59
4)OK
5)OK p
continue de remplir le tableau
6) applique la formule que tu as indiquée pour le calcul de E(X)
| Issues de xi | 0 | 6 | 10 |
| P(X = xi) | p1= 1-P(T)= 0,59 | p2= P(T C)= 0,14 C)= 0,14 | p3= P(T |
Si oui :
6. E(X)= 3,54
7. Si on répète un grand nombre de fois cette semaine, la recette hebdomadaire est d'en moyenne 3,54€.
Très bien, je vous remercie PLSVU de m'avoir aidée dans cet exercice et vous souhaite une bonne fin de journée🤗




