Inscription / Connexion Nouveau Sujet
Probabilité et Second degré
Bonjour,
Cela fait plusieurs jours que je travaille sur un dm, mais 2 de ses exercices me posent problème.
Pour le premier sur le second degré :
On considère les paraboles Pk qui a pour équation :
y = -x²+(2k-3)x-k²+2k+3 où k désigne un réel.
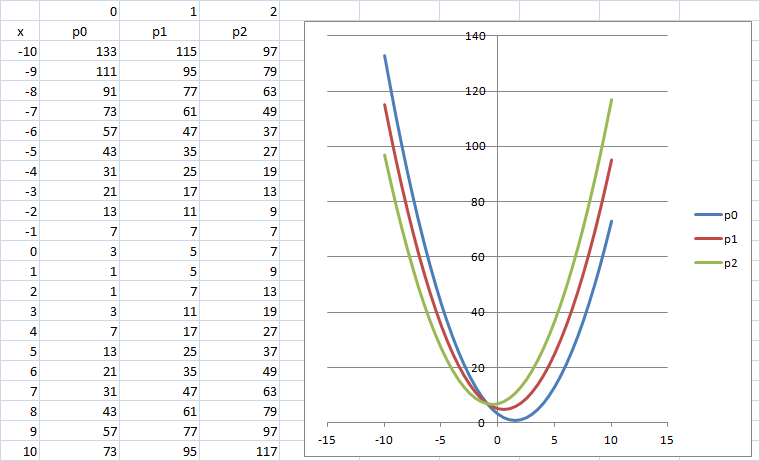
1) Tracer dans un repère les paraboles P0,P1,P2.
Quelle conjecture peut-on émettre sur les sommets de ces paraboles?
On remarque que les sommets sont de 1 plus bas en ordonné par rapport à la précédente, on peut émettre l'hypothèse que le coeff directeur est -1.
2)Donner les coordonnées des sommets de ces paraboles notés S0, S1, S2.
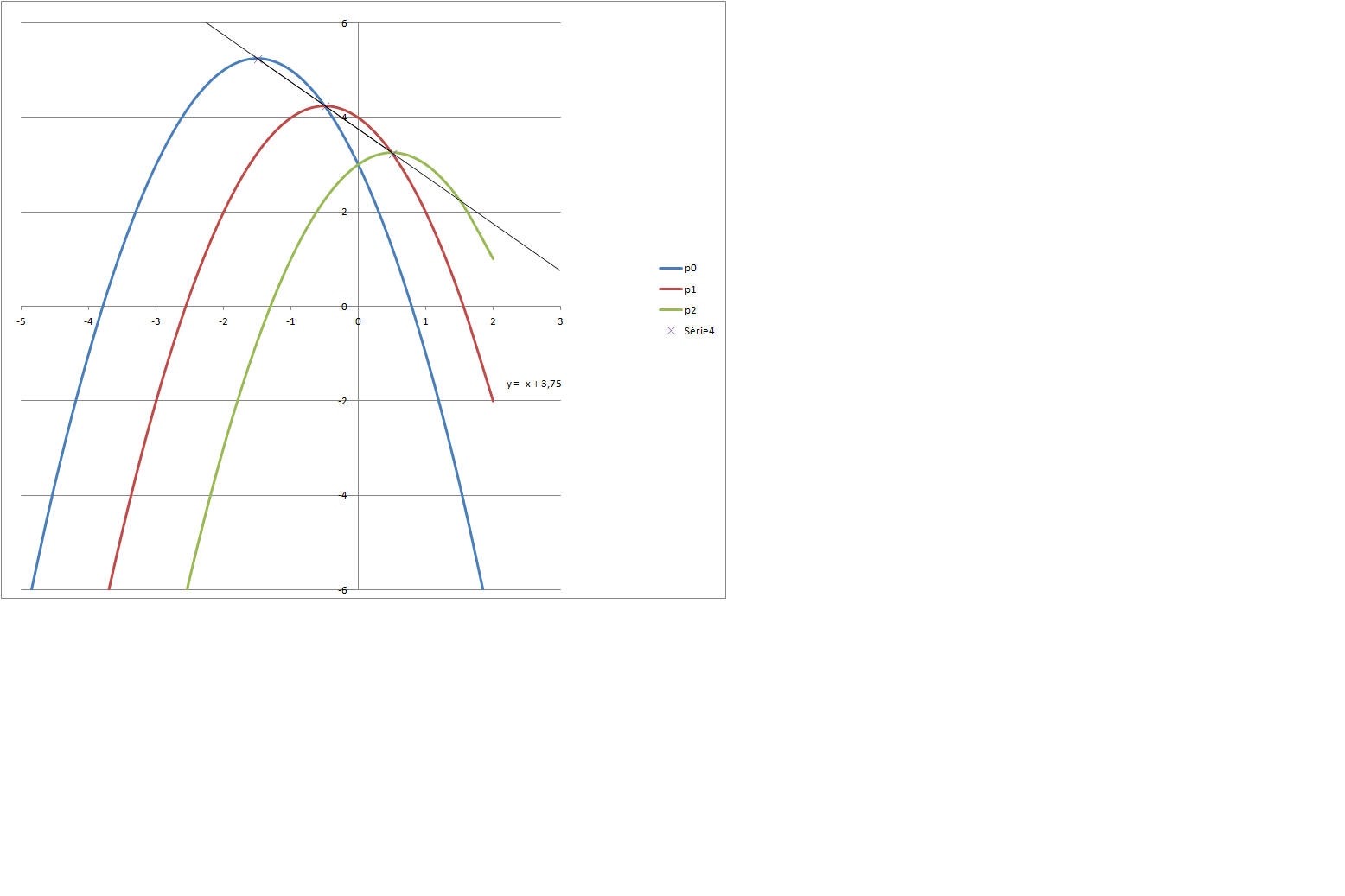
Déterminer une équation de la droite (S0S1) et prouver la conjecture émise au 1.
S0 : (-1,5;5,25) S1: (-0,5;4,25) S2 : (0.5;3,25)
équation d'une droite : ax+b
a= (4,25-5,25)/(-0,5-(-1,5))= -1
4,25= -1*-0,5+b
-b=0,5-4,25
b=3,75
ducoup on a : -1x+3,75
3) On note  l'abscisse du sommet S de la parabole Pk, exprimer
l'abscisse du sommet S de la parabole Pk, exprimer  en fonction de k.
en fonction de k.
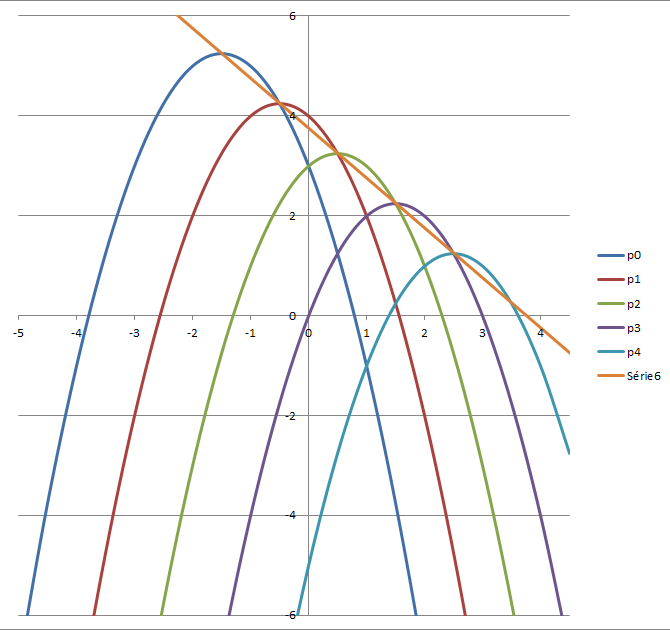
exprimer  en fonction de k et montrer que S appartient à la droite (S0S1)
en fonction de k et montrer que S appartient à la droite (S0S1)
Je ne vois pas comment faire, si quelqu'un pouvait m'aiguiller.
Merci pour votre aide.
Chacun son tour d'être désolé et confus 
Les 3 paraboles de mon précédent message ne sont pas les bonnes  : le terme -k² est passé à la trappe !! Evidemment je ne trouvais pas comme toi et les 3 sommets n'étaient pas alignés !!
: le terme -k² est passé à la trappe !! Evidemment je ne trouvais pas comme toi et les 3 sommets n'étaient pas alignés !!
Je vais essayer de faire mieux cette fois 
Question 2
Les coordonnées des 3 sommets sont exactes.
L'équation de la droite S0S1) est exacte.
La conjecture (hypothèse) que tu n'as pas vraiment clairement exprimée à la question 1 est que les 3 sommets sont.... alignés.
Il faudrait que tu montres que S2 est sur la droite (S0S1)
Question 3
 = ??
= ??
Pour la question 3
On part des résultats vus en cours de Seconde !
Les coordonnées du "sommet" S de la parabole d'équation y=ax²+bx+c sont
xS = = ??? (formule en fonction de a et b)
= ??? (formule en fonction de a et b)
et
yS = ????
Pour la parabole Pk, que valent (en fonction de k)  et
et  ?
?
Restera alors à vérifier que le sommet de Pk est SUR la droite (S0S1)
Je cherche je cherche, et j'en suis arrivé à alpha = (-2mx-3x-m)/-2
1) Non. alpha ne dépend pas de x.
Dans ton cours de Seconde tu devrais en principe trouver les formules suivantes :
Les fonctions polynômes du second degré qui à x font correspondre f(x) = ax²+bx +c sont représentées par des paraboles (dont l'équation est bien sûr y = ax²+bx +c). Le signe du coefficient de x² soit "a" donne le sens de variation de f [a négatif alors f croissante puis décroissante ; a positif alors ......].
Le sommet S a pour coordonnées xS ou
 = -b/(2a) et yS ou
= -b/(2a) et yS ou  = f(
= f( )
)
Tu connais l'expression de fk(x) donc tu dois pouvoir exprimer les coordonnées de Sk en fonction de... k.
2) Tu n'as pas répondu à :
Question 2
Les coordonnées des 3 sommets sont exactes.
L'équation de la droite S0S1) est exacte.
La conjecture (hypothèse) que tu n'as pas vraiment clairement exprimée à la question 1 est que les 3 sommets sont.... alignés.
Il faudrait que tu montres que S2 est sur la droite (S0S1)
Comment peux-tu démontrer cela ?
Dans le forme canonique du polynôme dus second degré ax^2+bx+c que l'on écrit a(x-alpha)^2+beta, alpha ne dépend pas de x, seulement des coefficients a et b. C'est du cours en seconde.
Je n'ai pas fais le second degré en seconde, mais c'est bon j'ai réussi à tout trouver et vérifier les résultats afin de savoir s'ils étaient bon, merci de votre aide!!