Bonjour je ne comprend pas l'énoncé d'un dm que je dois faire. Celui-ci étant
"On a placé dans un sac 10 jetons: des verts et des bleus. On tire deux jetons successivement avec remise. On note X la variable aléatoire associée au nombre de jetons bleus obtenus. On sait que p(X=1) =0.48. Le but de l'exercice est de trouver le nombre n de jetons verts présent dans le sac.

1) Quelles valeurs peut prendre n?
2) Combient y'a t'il alors de jetons bleus dans le sac, en fonction de n?
3) On tire un jeton du sac. Donner, en fonction de n, la probabilité d'obtenir:
a)un jeton vert
b)un jeton bleu
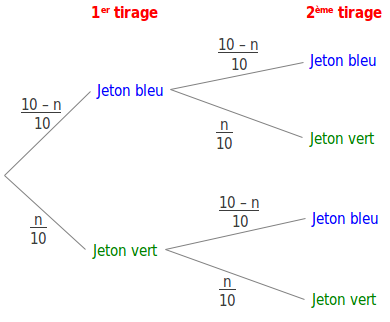
4)Représenter cette expérience par un arbre pondéré. En déduire p(X=1)en fonction de n
5)En déduire que n est solution de l'équation 2n²-20n+48=0
6)Répondre au problème posé

Pour la question 1), je pensais que n était compris entre 1 et 10 soit . Pour la 2): 10-n= Au nombre de jetons bleus
Pour la 3) je me suis aidée d'un arbre pondéré. a) soit E l'événement obtenir un jeton vert  P(E)= 1-0.48=0.52
b)Soit B l'évènement obtenir un jeton bleu P(B)= 0.48
Pour la 4 il suffit de faire un arbre avec deux issues indépendantes et identiques avec un succès et un échec. Pour ensuite en déduire P(X=1)= au coefficient binomiale sur la calculette avec les touches binomFDP(n,k,et la probabilité) qui est tout simplement P(X=k)=(n sur k) x (p^k) (1-p)^n-k

Merci de bien vouloir m'aider