Inscription / Connexion Nouveau Sujet
ProbabilitéS
Pouvez vous m'aider ?
On dispose de deux urnes.
La première urne contient 4 boules blanches et n boules rouges (n<6).
La seconde urne contient 2 boules blanches et (5-n) boules rouges.
On choisit au hasard une urne et une boules dans cette urne.
Déterminer n pour que la probabilité de tirer une boule rouge soit maximale.
AIDE: On donne le tableau de valeurs de la fonction f définie sur [0;5] par
f(x)= (x2-4x-10)/(x-4)(7-x)
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5/14 | 13/30 | 7/15 | 13/28 | 5/12 | 5/18 |
salut
P(R)=P(R/U1).P(U1) + P(R/U2).P(U2) = n/(4+n) * 1/2 + (5-n)/(7-n)*1/2
on obtient donc une fonction de n de type f(n)= n/(4+n) * 1/2 + (5-n)/(7-n)*1/2 et pour trouver
n tel que f soit maximale il suffit de deriver f et resoudre f'(n)= 0
f(n)'= u/v * 1/2 + u/v * 1/2 ???
= ((1(4+n)-n*1)/(4+n)^2)* 1/2 + ((-1(7-n)-(5-n)-1)/(7-n)^2) * 1/2 ????
Si on ne veut pas procéder avec la dérivée comme flight te l'as montré ( qui est la meilleure méthode si on n'a pas de tableau de valeurs ) , on cherche tout simplement la valeur de x ( qui est la même que celle de n ) qui donne la plus grande image f(x)
f(n) correspond à la probabilité d'obtenir une boule rouge suivant les valeurs n ( mais cela a été bien montré par flight )
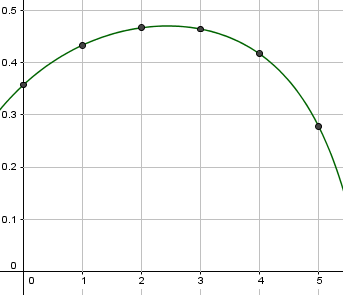
Regarde la représentation de cette fonction
Sur l'axe des x , tu as les valeurs de n
Les ordonnées des points sont les probabilités selon n de tirer une boule rouge
c'est donc aussi simple que ca ? car ma prof m'a dit "En mathématiques, "évident" est le mot le plus dangeureux." Eric Temple Bell
Du coup je sais pas comment faire...
Tu peux évidemment dériver -(x²-4x-10)/(x+4)(7-x) et étudier les variations de cette fonction .
A mon avis , le plus important dans cet exercice est ce que flight t'a expliqué dans le post de 13h30
Quand tu fais le calcul de probabilités , tu trouves cette relation
P(R)=P(R/U1).P(U1) + P(R/U2).P(U2) = n/(4+n) * 1/2 + (5-n)/(7-n)*1/2 = f(n)
Que l'on marque x ou n revient au même . Ici , cette fonction n'existe que pour des valeurs entières des antécédents . C'est pourquoi sur la courbe , je t'ai marqué des points
Bonjour, j'ai le même énoncé excepté que je n'ai pas k'aide avec la fonction et la tableau, j'aurais besoin d'aide pour dériver la fonction f(n) que j'ai réussi à retrouver.
J'ai trouvé la dérivée suivante : f'(n)= 4/2(4+n)² + 12/2(7-n)² est-ce bon ? Comment puis-je faire pour faire mon tableau de signe après ça ?

 :?
:? 0,278
0,278

