Inscription / Connexion Nouveau Sujet
Probabilités
Bonjour, je m'entraîne à la vue d'un prochain bac blanc et je bloque sur les deux dernières questions. Si quelqu'un pouvait m'aider... merci d'avance
Dans un pays imaginaire, on admet qu'un jour donné soit il fait beau, soit il pleut.
S'il fait beau un jour, alors il fera beau le jour suivant avec une probabilité égale à 1/2.
S'il pleut un jour, alors il pleuvra encore le lendemain avec une probabilité de 2/3.
Aujourd'hui il pleut.
On s'interesse à laprobabilité qu'il fasse beau demain, dans 2 jours, dans 3 jours, ... dans n jours.
1. Pour n=>1, on désigne par Bn, l'évènement "il fera beau dans n jours" et pn la probabilité de Bn
1. Illustrer par un arbre pondéré, l'évolution possible de la météo pour demain et après demain.
2. Déterminer les valeurs exactes de P(B2) et p(B3)
3.Démontrer que, pour n1, P(Bn+1)=1/6*P(Bn)+1/3.
4. On pose désormais, pour n1, Pn=P(Bn) et Un=Pn-2/5.
a. Prouver que (Un) est une suite géométrique de raison 1/6
b. En déduire l'expression de Un, puis de Pn en fonction de n, pour n1.
5. Estimer la probabilité qu'il pleuve le 1000eme jour.
Pour la 4.a. J'ai trouvé:
Un+1=pn+1-2/5
=1/6pn+1/3-2/5 Grâce aux résultats de la question précédente
=1/6pn-2/30
=1/6(pn-2/5)
=1/6un
Je pense que pour trouver l'expression de un et pn ça doit être un truc tout bête... mais je ne trouve pas
Pour la 5. par contre je n'ai vraiment aucune idée
Voila, merci d'avance.
salut
"Bn" pour beau le jour n et "nonBn" il pleut le jour n
P(Bn+1/Bn)= 1/2
P(nonBn+1/nonBn)=2/3
P(Bn+1)=P(Bn+1/Bn).P(Bn)+P(Bn+1/nonBn).P(nonBn)
avec P(Bn+1/Bn)=1/2
P(Bn+1/nonBn)= 1-P(nonBn+1/nonBn)
donc P(Bn+1)= 1/2*P(Bn)+ (1-2/3)*P(nonBn)= 1/2*P(Bn)+ (1-2/3)*(1-P(Bn))
P(Bn+1)= 1/2*P(Bn)+ (1/3)*(1-P(Bn)) = 1/6*P(Bn) + 1/3
..en posant P(Bn+1)=Pn+1
alors Pn+1 = 1/6*Pn + 1/3
comme Pn= Un + 2/5 alors
Un+1+2/5 = 1/6(Un+2/5)+ 1/3 soit Un+1= 1/6.Un
et donc Un = (1/6)^(n-1) *U1 comme U1 = P1-2/5 = 0-2/5 = -2/5
alors Un = -2/5*(1/6)^(n-1) alors Pn = Un + 2/5 = -2/5*(1/6)^(n-1) + 2/5 =
2/5.(1-(1/6)^(n-1) ) donc Pn = 2/5.(1-(1/6)^(n-1) ) sauf erreur
Pour moi, d'après l'énoncé:
P1=P (B1)
Donc P(B1)=1/3 et par conséquent U1=1/3-2/5=-1/15
C'est justement ici que je trouve bizarre de trouver un nombre négatif... comme dans tes résultats d'ailleurs
Selon moi on obtient l'arbre ci dessous. En effet on sait qu'aujourd'hui il pleut donc c'est P(B0) qui vaut 0 et non P(B1) puisque celui ci correspond à demain
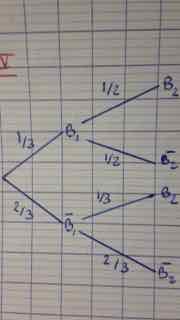
D'accord merci. Donc pour la dernière question je remplace n par 1000 dans l'expression de Pn je trouve:
Pn=-1/15*(1/6)^(1000-1)+2/5
=0.4
Donc on a ici la probabilité qu'il fasse beau le 1000eme jour. Donc pour trouver la probabilité qu'il pleuve on fait simplement 1-Pn c'est ça ?
Ainsi |p1000=1-0.4=0.6


