Inscription / Connexion Nouveau Sujet
Probabilités
Bonjour à tous, je dois donc rendre un DM pour mardi mais il me reste un exercice.
Voici l'énoncé:
On lance un dé dont les faces sont numérotées de 1 à 6. On définit une variable aléatoire X en associant à chaque tirage le nombre: •- 5 si on tire le numéro 1
•0 si on tire les numéros 2,3,4,ou 5
•10 si on tire le numéro 6
1) définir l'ensemble des événements élémentaires
2) donner l'ensemble des variables aléatoires
3) on suppose le dé parfaitement équilibré
A) donner la loi de probabilité de X
B) calculer l'espérance mathématique
4) on suppose que le dé est truqué et que les probabilités d'apparition des numéros 1,2, 3,4 et 5 sont toutes les cinq égales à 0,14
A) donner la loi de probabilité de X
B) calculer l'espérance mathématique
5) on lance maintenant les deux dés l'un après l'autre on associe toujours les mêmes valeurs que précédemment.
A) donner la loi de probabilité de X
B) calculer l'espérance mathématique
6) que peut-on en déduire?
J'ai pensé pour la 1) écrire:
-5 = 1 sur 6
0 = 4 sur 6
10= 1 sur 6
2) j'ai fais un tableau en remettant mes valeurs soit X et p(x=....)
Et après je ne sais plus comment m'y prendre
Merci d'avance pour votre aide 
Bonjour,
Pour la première question c'est tout faux.
Il fallait répondre que l'ensemble des évènements élémentaires est {-5; 0; 10}
ou, peut-être {1, 2, 3, 4, 5, 6} mais sûrement pas que -5 = 1/6 !!!
En réalité, tu as voulu écrire que p(X=-5) = 1/69 ... mais ce n'est pas du tout ce que tu as écrit et ce n'est pas ce qu'on demandait.
Pour la 2e question, il doit y avoir une coquille dans le texte : ce n'était pas plutôt Donner l'ensemble des valeurs prise par la variable aléatoire ?
Merci de votre réponse.
Je ne comprends pas pourquoi p(x=-5)= 1/69...
Pour la deux pourtant c'est bien ce qui est écrit mais vous devez sûrement avoir raison.
Je me suis trompé à mon tour (j'ai les doigts trop gros). Tu as voulu écrire p(X=-5)=1/6.
Pour la seconde question, il n'y a qu'une variable aléatoire, donc il s'agit d'une erreur dans le texte.
Tu dois recopier ton texte : relis la charte du forum ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
Cela dit, le texte, même tapé à la machine, n'a pas plus de sens. Il fallait dire Donner l'ensemble X( ).
).
On peut donc en déduire que pour la première question il fallait donner l'ensemble des évènements élémentaires :  ={1, 2, 3, 4, 5, 6}.
={1, 2, 3, 4, 5, 6}.
Bonjour, j'aimerai relancer ce sujet car je suis réellement bloquée sur cet exercice. 
Merci d'avance pour votre aide.
À partir de quelle question es-tu bloquée ?
Je suppose qu'à la première question, tu as répondu que l'ensemble des évènements élémentaires est  ={1, 2, 3, 4, 5, 6}
={1, 2, 3, 4, 5, 6}
La question 2, très mal recopiée, te demande (probablement) de donner l'ensemble des valeurs prises par X, qu'on appelle X( ).
).
Il fallait répondre : X( )={-5, 0, 10}
)={-5, 0, 10}
Es-tu allé au-delà de cette question ?
Merci énormément d'avoir répondu.
Alors justement j'ai seulement répondu à ces deux premières questions c'est par la suite que je suis bloquée...
Je ne comprends pas réellement ce qu'il faut écrire.
Pour la question 3a) il faut faire un tableau montrant la distribution des probabilités suivant les différentes valeurs prises par X :
| k | -5 | 0 | 10 |
| p(X=k) | ... | ... | ... |
Ah d'accord je vois et je sais réaliser l'espérance mathématique merci beaucoup!
Mais plus bas c'est ici que je ne comprends pas avec le dé truqué et le lancé des deux dés.
Le dé est truqué de telle sorte que les probabilités des 6 faces ne sont pas toutes égales. Les 5 premières faces ont une probabilité d'apparition égale à 0,14. Tu peux en déduire la probabilité d'apparition de la face 6.
Non : la somme des probabilités des évènements élémentaires est égale à 1, mais la face 6 n'a pas une probabilité aussi grande...
Pour la question 5, on change d'expérience puisqu'on utilise 2 dés (le dé normal et le dé truqué je suppose). Que représente alors la variable X ? La somme des 2 dés ? Ton énoncé n'est pas clair ici.
La variable X représente alors la somme des 2 dés, mais la somme est alors égale à par ex :
1er dé: p(x=1)= 1/6
2ème dé: p(x=1)= 0.14
Donc comment dois-je procéder?
Je suppose que la variable X représente la somme des 2 gains des 2 tirages (certains gains étant négatifs).
Il y a donc 7 valeurs possibles (-10, -5, 0, 5, 10, 20) :
| -5 | 0 | 10 | |
| -5 | -10 | -5 | 5 |
| 0 | -5 | 0 | 10 |
| 10 | 5 | 10 | 20 |
Il faut calculer les différentes probabilités liées à ces 7 valeurs et faire un tableau de distribution comme pour la question 3a)
Il est tard, je vais devoir arrêter. Désolé. Tu dois pouvoir te débrouiller pour finir ...
Voici une autre manière de représenter l'expérience aléatoire de la question 5.
Le premier dé est équilibré : chaque face a la même probabilité 1/6. La variable aléatoire X qui lui est associée vaut :
• -5 si la face est 1. On a p(X=-5)=1/6
• 0 si la face est 2, 3, 4 ou 5. On a p(X=0)=4/6
• 10 si la face est 6. On a p(X=10)=1/6
Le second dé est truqué. La variable aléatoire Y qui lui est associée vaut :
• -5 si la face est 1. On a p(Y=-5)=0,14
• 0 si la face est 2, 3, 4 ou 5. On a p(Y=0)=4 0,14=0,56
0,14=0,56
• 10 si la face est 6. On a p(Y=10)=0,3
La variable aléatoire finale est Z=X+Y. Ses valeurs sont affichées en bleu sur l'image. Il te reste à trouver les probabilités ...
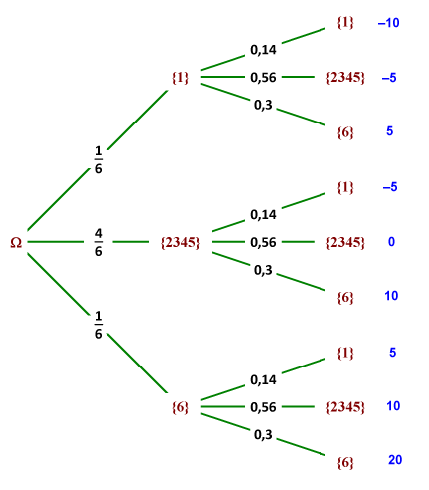
Super ! Je comprends cet arbre mais comment "trier" en quelque sorte les probabilités car j'ai essayé hier et lorsque j'ai tout retranscrit la somme des probabilités dans le tableau du lancé des 2 dés (celui normal et celui truqué) la somme n'était pas égale à 1
Pour obtenir, par exemple, la probabilité de l'évènement (X=-5; Y=-5), il suffit de faire le produit des probabilités marquées sur les branches :
(c'est la première branche en haut de l'arbre)
Comme il n'y a qu'un seul cas où X+Y=-10, on peut dire que P(X+Y=-10)=7/300
Par contre, il y a plusieurs cas où X+Y=5. Dans ce cas, il faut ajouter les probabilités de chaque cas.
La somme des probabilités des 9 branches doit être égale à 1.
Les probabilités des évènements sont toutes exprimables par des fractions dont le dénominateur est 300, en effet, mais certaines peuvent se simplifier. Prends ta calculatrice pour faire les calculs...
Par exemple, .
Le total des probabilités doit être égal à 1. Sinon, tu t'es trompé dans les calculs.


