Inscription / Connexion Nouveau Sujet
Probabilités
Bonsoir !
J'aurais besoin d'un œil avisé pour une possible correction et un peu d'aide pour la dernière question pour laquelle je ne suis pas sure de la réponse 
Voici l'énoncé :
Pour se rendre dans le centre-ville, Bruce peut prendre deux chemins :
- L'un passe une fois au-dessus du fleuve de sorte qu'il faut passer sur un pont P1 dont la probabilité d'être fermé est 0.2, auquel cas, il ne peut pas se rendre au centre-ville.
-L'autre passe deux fois au-dessus du fleuve de sorte qu'il faut passer sur deux ponts P2 et P3 dont les probabilités d'être fermés sont 0.1 (on admet alors que la fermeture ou non d'un pont est indépendante de l'autre et du chemin emprunté par Bruce). Si au moins l'un des deux ponts est fermé, il ne peut pas se rendre au centre-ville.
Quand Bruce va au centre-ville, il passe par le premier chemin 80% du temps (sans avoir d'information sur le fait que les ponts soient ouverts ou non).
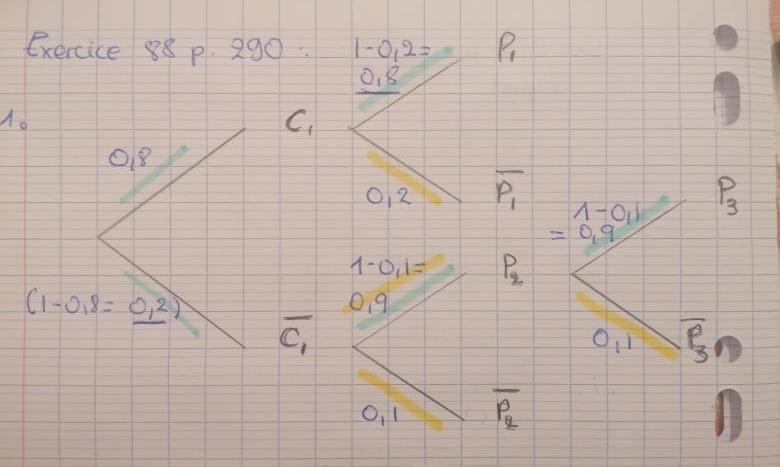
1. Compléter l'arbre pondéré (cf. image jointe).
2. En admettant qu'on peut utiliser les règles classiques sur les arbres pondérés, déterminer la probabilité que Bruce soit bloqué par un pont.
3. Bruce est bloqué par un pont. Quelle est la probabilité qu'il ait pris le premier chemin ?
2. p(P barre) = p(CinterP1 barre) + p(C1 barre inter P2 barre) + p( C1 barre inter P2 inter P3 barre)
= (0.8*0.8)+(0.2*0.1)+(0.2*0.9*0.1)
= 0.678
Soit p(P barre) 0.68
0.68
3. p P barre( P1) = p(Pbarre inter P1) = p(P barre inter P1)/ p(P barre) = (0.2*0.8)/0.678 =0.236
Voilà, merci d'avance pour votre aide !
bonsoir,
pour toi l'évènement P1 c'est Pont 1 Ouvert ?
si oui,
p(P barre) = p(CinterP1 barre) + p(C1 barre inter P2 barre) + p( C1 barre inter P2 inter P3 barre)
= (0.8*0.8)+(0.2*0.1)+(0.2*0.9*0.1)
je crois que c'est 0.2 au lieu de 0.8, là...
Oui excusez-moi, une erreur inattention malheureusement ...
Donc p(P barre) = 0.198 maintenant et ;
2. p P barre (P1) = 0.808
Correct ?
salut
ces resultats me semblent bizarre , à moins de n'avoir pas compris l'enoncé
sur le chemin 1 , on a un seul pont qui est ouvert avec une proba de 0,8
sur le chemin 2 , on a un deux pontx qui sont ouverts avec une proba chacun de 0,9
je dirais que la proba d'etre bloqué à un pont avec l'evenement" B" pour bloqué :
P(B)=P(B/chemin1).P(chemin1)+ P(B/chemin2).P(chemin2)
P(chemin1)=0,8
P(chemin2)=0,2
P(B/chemin1)=0.1
P(B/chemin2) = P( au moins un point est fermé sur le chemin 2 ) =
0,1 + 0,1 - 0,1² = 0,19 qu'on peut retrouver aussi en ecrivant p2 fermé et p3 ouvert
ou p2 ouvert et p3 fermé ou p2 et p3 fermés soit 2*0.1*0.9 + 0.1² = 0.18 +0.01 =0.19
et donc P(B)= 0.1*0.8 + 0.19*0.2 = 0.118
qu'en dis tu Leile ?
bonjour flight,
je vois ce que tu veux dire, mais
p(B / C1) = 0,2 (et non 0,1 ) (faute de frappe ? ) " pont P1 dont la probabilité d'être fermé est 0.2"
et pour moi, sur le C2, les ponts sont empruntés l'un après l'autre.
Si P2 est fermé, on n'ira pas plus loin, même si P3 est ouvert.
donc
bloqué = C1 et P1 fermé + C2 et P2 fermé + C2 et P2 ouvert et P3 fermé
p(B) = 0,2 * 0.8 + 0.2*0.1 + 0,2*0.9 * 0.1 = 0.198
j'ai compris l'énoncé comme ça, mais je peux me tromper aussi
 :)
:)
Pour ma part, c'est plus la réponse de la question 3 qui me trouble... Ne devrions-nous pas utiliser un système à 3 équations de 3 inconnues ?
Nous savons que Bruce emprunté un pont fermé, donc p(P barre) =0.198 si je me souviens bien.
Et nous voulons savoir quelle est la probabilité que Bruce est emprunté le Chemin C1 et donc P1 barre...
Peut-être sur c'est juste moi qui me fait des idées, mais bon ça me paraît trop "simple" de résoudre cette question simplement avec une probabilité conditionnelle...
flight
Dans l'énoncé, il est bien dit que la probabilité qu'un pont doit fermé est indépendant d'un autre pont... Donc ce que j'ai écris précédemment et ce que Leile a réaffirmé me semble correct...
Bon, chacun fait des d'autre, donc dès que j'aurais la correction, je reviendrai pour préciser 
Bonjour,
Juste pour essayer de vous rassurer :
Le prof va vraisemblablement faire une correction qui utilise l'arbre, sans se poser plus de question.
Peut-être aura-t-il prolongé la branche d'extrémité ; ce qui ne sert à rien.
L'autre raisonnement me semble tout aussi correct. Il donne bien le même résultat une fois la coquille rectifiée 
Sylvieg
Bonjour,
Je viens donner suite au sujet. Apparemment mon cheminement était juste ! Le vôtre est conséquemment juste aussi 
Passez une bonne journée et merci pour vôtre intervention.
Merci claudinelyon d'avoir donné suite 
Mais je m'interroge sur le côté réalisable du contexte :
Pour aller de D, le départ, à C, le centre ville, Bruce peut traverser une ou deux fois le même fleuve.
Essayez de faire un croquis...
A moins que le fleuve se sépare en deux à un moment, je ne vois pas bien la configuration.
Ou alors la source est par là ?



