Inscription / Connexion Nouveau Sujet
Problème.( 2 )
bonjour,
voila encore un problème avec encore une figure géométrique donc je vais essayer d'être précis car cette est assez compliquée:
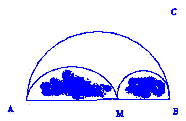
" C est un demi-cercle de centre O, de rayon R= AB/2.
M est un point de [AB]. à l'intérieur de C on trace deux demi-cercle de diamètre [AM] et [MB]."
1) L'aire de la partie hachuréé ( le demi-cercle AM et MB) peut elle être égale à la moitié de l'aire du demi disque?
2) Comment placer M pour que l'aire de la partie hachurée soit maximale ?
Voila si quelqu'un veut pour m'aider le dessin de la figure mon msn: ***
ou mon mail: sp2b@netcourrier.com
Voila merci pour votre aide .
voila c'etait juste pour dire que la figure fallait la faire sachant que c'est le debut de l'exercice donc je n'ai pas reproduit quelque chose ou autre... voila merci. plz aidez moi
Tom pascal est ce que tu pourrai edit aussi le dessin de ce problème stp merci pour ton aide comme ca j'espere que quelqu un pourrait m'aider a repondre aux questions.
Bonjour,
AM=x
Aire hachurée=A
A= x²/8+
x²/8+ (2r-x)²/8
(2r-x)²/8
A= (x²-2rx+2r²)/4
(x²-2rx+2r²)/4
1)
A= r²/4 équivalent à
r²/4 équivalent à
x²-2rx+2r²=r²
(x-r)²=0
x=r (M milieu de [AB])
2)
A max ssi y=x²-2rx+2r² max
ssi x=r (en étudiant le signe de y'=2x-2r ou en utilisant un résultat de cours (ax²+bx+c passe par un extremum pour x=-b/2a...))
L'aire max est donc celle trouvée au 1.
A vérifier...
merci mais je comprend pas trop ce que tu as ecris sachant que je n'ai jamais fais ca pourrai tu t expliquer avec les détails merci
Re !
Alors je reprends pour le calcul de l'aire hachurée : c'est la somme des aires des deux demi-cercles intérieurs.
On utilise le fait que l'aire d'un demi cercle de rayon r :
--> le demi-cercle le plus à gauche est de diamètre [AM]. Donc avec les notations de Dasson, il est de rayon
Donc son aire est .......
--> le demi-cercle le plus à droite est de diamètre [MB].
Or M appartient à [AB].
Donc (cas d'égalité de l'inégalité triangulaire) .
Sachant que AB = 2.R (R rayon du grand demi-cercle extérieur), MB = 2.R - AM
Donc
Donc son aire est .......
--> L'aire hachurée est la somme des deux résultats trouvés plus haut
erff voila et en faite bon une fois que l'on trouve le résultats de l'aire hachurée comment peut on savoir si elle peut être égale a la moitier de l'aire du demi cercle ? donc si on a l aire hachurée comment trouve prouve t on que l'aire des cercles hachuré peu etre egale a la moitier de demi cercle ?
Tu sais, Carpe, Dasson t'as donné une réponse brève (ce que je ne sais pas faire  ) mais complète !
) mais complète !
As-tu essayé de reprendre sa réponse ?!
Entre ta réflexion et sa réponse... tu aurais du trouver !
Bon, je reprends un peu avec toi le raisonnement à suivre :
On se demande s'il se peut que .
On est donc amené à résoudre l'équation en x
Je te laisse faire...
@+
Emma
bonjour,
je cherche la formule qui me servirai a calculer l'aire d'un demi cercle ?
*** message déplacé ***