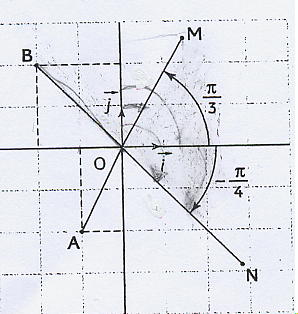
Bonjour,

Toutes tes coordonnées (polaires ou cartésiennes) sont fausses

Il ne me semble pas que ce soit des fautes de frappe. Alors on va reprendre cela et je suis sûr que tu vas comprendre.

Tout d'abord le point M
Nous sommes bien d'accord que la longueur OM vaut 3 et que (

Quelles sont les coordonnées polaires (les plus faciles à déterminer) et quelles sont les coordonnées cartésiennes ?

:S.

Merci pour ton aide.
Alors les coordonnées polaires de M sont (3, pi/3), et les coordonnées cartésiennes de M sont (3/2; (3rac3)/2) ?

Même travail avec le point N

En fait, j'ai trouvé mon erreur je n'ai pas pris (i, OM) en vecteurs, mais (j,Om) ^^.
Alors, avec le point N je trouve comme coordonnées polaires (4;-pi/4), et comme coordonnées cartésiennes (2rac2;-2rac2).

Coordonnées polaires du point B et conclusion sur l'alignement des points B, O et N

=D.

Alors, on voit sur la figure que les coordonnées cartésiennes de B sont (-2;2), donc :
r=4 et teta=3pi/4.
Donc, les coordonnées polaires de B sont (-2rac2;2rac2) ?
Mais pour montrer l'alignement je ne sais pas comment faire...

Pour le point B, r n'est pas égal à 4 (théorème de Pythagore )

Oui pour le point B, _B = 3/4

Alignement :
Quelle est la différence entre _N et _B ?
Qu'en penses-tu ?

HANN, je sais plus compter.
R ne serait pas égal à 2rac2 ?? Et, si c'est la cas, alors les coordonnées polaires de B sont (-2;2) ??

Et, on peut dire que N et B sont opposés diamétralement, donc [BN] passe par l'origine, donc les points O, B et N sont bien alignés.

C'est mieux... tu confonds encore le vocabulaire ; fais bien attention !

Coordonnées polaires de B :

Coordonnées cartésiennes de B : (-2 ; 2)

Oui, d'accord pour ta démonstration de l'alignement de B, O et N

Troisième question ?

Ah oui, mince, j'ai mis coordonnées polaires :S.
Merci =D.


J'vais faire la troisième question.

J'ai trouvé un début ^^, mais je bloque

Si les points O, A et M sont alignés, alors :

(OA, OM) = o (2pi) ou (OA, OM) = pi (2pi).

Et là, je n'arrive pas à trouver la mesure de l'angle.

Bonsoir
on te dit d'utiliser les coordonnées cartésiennes pour cette question (autrement dit, tu peux utiliser une équation de la droite (OM))

Tu pourrais faire comme cela (ce serait à mes yeux le plus simple) mais ce n'est pas ce que te demande l'énoncé :

Bonsoir lafol

bonsoir, coll

Oui, justement, c'est ça qui me pose problème, c'est d'utiliser les coordonnées cartésiennes :S.
Je ne vois vraiment pas comment on peut justifier que les points ne sont pas alignés avec les coordonnées cartésiennes.

Pour M, y = racine(3) x.
Pour O aussi
Si A est aligné avec eux, ses coordonnées doivent vérifier la même équation

Plusieurs méthodes :

. Faire comme l'a dit lafol : par exemple montrer que le point M n'est pas sur la droite OA
Pour cela déterminer l'équation de la droite OA et montrer que les coordonnées (que tu connais) du point M ne sont pas celles d'un point de la droite.

. Montrer que les vecteurs et ne sont pas colinéaires.

Merci beaucoup pour votre aide =D.

Donc, si j'ai bien compris, pour A, y =2x, donc ses coordonnées ne vérifient pas la même équation.

Par contre, lafol, je ne comprend pas ce que tu veux dire par "Pour O aussi".

La droite OA est bien la droite d'équation y = 2x

le point M de coordonnées M : (3/2 ; (1/2)33) n'est pas un point de cette droite puisque (1/2)33 3

O = racine(3) fois 0

Ah d'accord !!
Bah je vous remercie d'avoir passé autant de temps à m'aider, parce que sinon, je ne sais pas comment j'aurai fait =D.
A bientôt.

Pour ma part, je t'en prie.
A une prochaine fois !

je n'ai presque rien fait
j'ai juste trouvé une occasion de saluer Coll

Merci lafol...
Mais si tu as fait quelque chose ; tu es arrivée juste à temps pour indiquer la solution la plus simple. Je ne sais pourquoi, mais j'aurais conseillé l'absence de colinéarité. Une fois de plus... "Deux lampes... moins d'ombre" ! J'aime vraiment cette formule ; et c'est une belle manière de voir le forum.