Inscription / Connexion Nouveau Sujet
Problème arc de cercle et angle
Bonjour à tous.
On donne la situation suivante :
on a un segment de 2cm relié à un arc de cercle de 3cm dont le rayon est égal à 2cm puis un autre segment reliant l'autre extrémité de l'arc. L'arc forme un angle au centre dont je dois calculer la mesure en degrés. Le premier segment est perpendiculaire au rayon de l'arc, idem pour le second.
Mon problème est que je n'arrive pas à calculer l'angle.
J'ai pensé à un rapport de proportionnalité entre le périmètre du cercle que je peux calculer (P = 4Pi) dont la mesure de l'angle serait de 360° et la mesure de mon arc de cercle de 3cm, soit :
4Pi cm = 360°
3cm = x°
x = 350x3/4Pi
Est-ce la bonne méthode ou est-ce possible d'utiliser un théorème, comme Pythagore ou les cosinus (ou les radians même si je ne sais pas encore comment ça marche)?
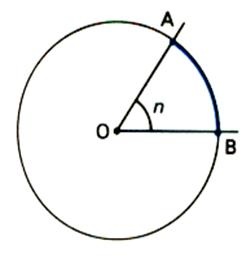
Je ne suis pas en mesure de faire une figure mais on va considérer celle que j'ai jointe.
On s'occupe uniquement de l'arc de cercle AB. On image un segment de 2cm perpendiculaire au côté [OA], de même, du côté [OB] et je dois calculer n.
Si le rayon est 2 , la circonférence (360°) est égale à 2 r soit 4
r soit 4
L'angle n vaut donc 3*360/4 = 85,94°
= 85,94°
Bonjour à vous deux
Pyro33
Si j'ai bien compris OA=OB=R=2 cm
Calcules la longeur x cm de la circonférence, x= ∏D (D=2R) qui correspond à un angle de 360°
pour une longueur x cm on a 360° pour 1 cm, x fois moins et pour 3 cm, 3 fois plus, ce qui se traduit par 360°*3/x= ? °
On obtient 85,94 degrés.
Mais est-ce possible de calculer cet angle avec les cosinus, sinus ou avec Pythagore?
Parce que je ne comprends pas quel est l'intérêt de nous dire qu'on a 2 segments perpendiculaires à [OA] et [OB].
Le premier segment est perpendiculaire au rayon de l'arc, idem pour le second
Effectivement , cette phrase est pas très compréhensive . Mais elle ne dit pas
qu'on a 2 segments perpendiculaires à [OA] et [OB]
Peut-être c'est pour indiquer qu'on a affaire à des rayons d'un même cercle .
Voilà, c'est une figure dans ce genre. On a un segment, l'arc de cercle puis un autre segment. Pythagore n'est donc pas utile dans ce cas? Ni les cosinus et sinus?
Non ,
Pythagore n'est donc pas utile dans ce cas? Ni les cosinus et sinus?
La solution t'a déjà été donnée :
Si le rayon est 2 , la circonférence (360°) est égale à 2r soit 4
L'angle n vaut donc 3*360/4= 85,94°