Inscription / Connexion Nouveau Sujet
Problème compréhension angles orientés
Bonsoir,
Malgré mes efforts pour essayer de comprendre ma partie de leçon concernant les angles orientés, je ne comprends toujours pas comment trouver les mesures principales. J'ai un gros DS la semaine prochaine sur la trigo et mon enseignant n'est pas vraiment là pour m'aider... Je n'arrive pas notamment à trouver la mesure d'un angle dont les vecteurs n'ont pas la même origine (ex: (AB,CD) ). Pouvez-vous m'exliquer, m'éclairer, me donner quelques astuces s'il-vous-plaît ?
Merci énormément.
Bonjour,
en fait la notion de vecteurs vue au collège et lycée est faussée.
en vrai un vecteur n'a pas "d'origine"
c'est un des nombreux représentants de ce vecteur qui en a une ...
ce qui permet d'écrire voulant bien dire que
et
sont réellement le même vecteur (des représentants différents du même vecteur)
donc quels que soient les représentants choisis, l'angle des vecteurs eux même sera le même.
si alors l'angle
"de façon triviale" et quel que soit
(parce que
et
sont réellement le même vecteur)
donc ne pas se poser de questions oiseuses sur les origines des vecteurs.
quand on écrit par exemple des relations de Chasles sur des angles, on se fiche complètement de savoir les "origines" des vecteurs, si c'est la même ou pas, c'est complètement indifférent.
ceci dit, sans énoncé / exemple précis à se mettre sous la dent on discute dans le vide ...
D'accord, merci. Je voulais ajouter un exo qui me posait un peu problème, cependant n'arrivant pas à insérer la figure, j'ai abandonné. Je poste quand-même l'énoncé :
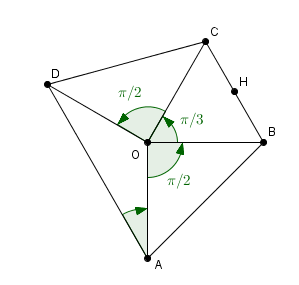
OBC est un triangle équilatéral tel que :
(OB,OC) = π/3
AOB et DOC sont deux triangles rectangles isocèles tels que :
(OA,OB) = (OC,OD) = π/2
H est le milieu du segment [BC]
1) Trouvez les mesures principales de :
c) (AD,AO)
Ma réponse : π/4 ?
d) (AB,CD)
Ma réponse : π/8 ?
2) Démontrez que les droites (AD) et (OH) sont perpendiculaires.
on peut faire ça "de façon élémentaire" en calculant les angles "ordinaires" et en déterminant le signe à part
donc ici l'angle = 2
 -
-  /2 -
/2 -  /3 -
/3 -  /2 = 2
/2 = 2 /3
/3
puis dans le triangle isocèle AOD l'angle à la base = (
 - 2
- 2 /3)/2 = ... certainement pas
/3)/2 = ... certainement pas  /4 et de toute façon le signe n'est pas bon.
/4 et de toute façon le signe n'est pas bon.
mais bof ...
ça devrait se faire avec les angles orientés et les relations de Chasles (tout en vecteurs)
on obtient immédiatement (OA; OD) = (OA;OB) + (OB;OC) + (OC;OD) + 2k (Chasles)
(Chasles)
et en remplaçant par les valeurs de l'énoncé (OA; OD) = -2 /3 + 2k
/3 + 2k
la relation de la somme des angles d'un triangle s'écrit en angles orientés
(AD; AO) + (OA; OD) + (DO; DA) =  +2k
+2k
d'où on tire 2(AD; AO) =  + 2
+ 2 /3 + 2k
/3 + 2k
et finalement (AD; AO) =  /2 +
/2 +  /3 + k
/3 + k = ...
= ...
(k = -1 pour avoir une valeur cohérente avec des angles d'un triangle)
on fait du même genre pour les autres questions.
bonjour à vous deux
Je n'arrive pas notamment à trouver la mesure d'un angle dont les vecteurs n'ont pas la même origine (ex: (AB,CD) ).
Voici deux vecteurs
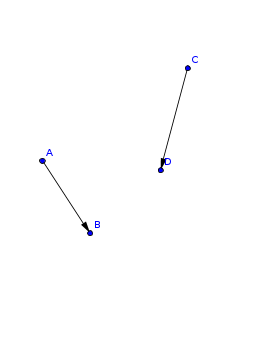
Si tu veux te représenter l'angle (AB,CD), prends un point n'importe où dans ta feuille, et à partir de ce point (j'ai pris le point E ici) tu redessines des vecteurs égaux aux précédents, ce qui donne
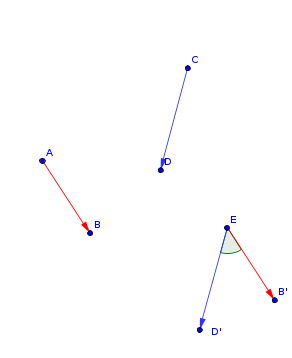
et l'angle que tu cherchais à lire est donc (EB' , ED')


