Inscription / Connexion Nouveau Sujet
Problème d'une échelle sur un mur
Bonjour,
Désolé de remettre ce topic d'actualité mais euh cette fois si cet éxo a été remanié pour une classe de première et j'ai réussi à m'en sotir pour le début mais j'aurai besoin de quelque pistes pour terminer...
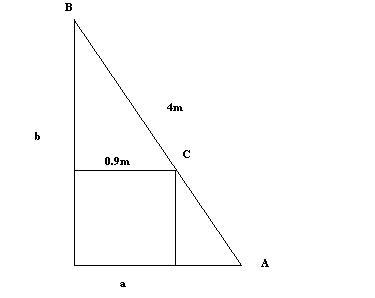
Une échelle de 4m est contre un mur en A et B et contre un cube en C de côté 0.9m
On me demande de calculer de calculer la hauteur du mur depuis le sol à l'échelle (b) et la longueur au sol séparant le mur de l'échelle (a)...
Avec Pÿthagore et Thalès j'ai trouvé: (ab)-0.9(a+b)=0 et 16= b²+a² mais je n'arrive pas à trouver une piste pour cette deuxième expression...
Je voudrai juste un peu d'aide...
bonjour
si H est le troisième point du triangle et I la projection de C sur BH et K la projection de C sur AH
BI/IC = CK/KA => (b-0,9) / 0,9 = 0,9/(a-0,9)
(10a-9)(10b-9) = 81
et
a² + b² = 4²
a = ( 9 + 81/(10b-9) )/10
que tu remplaces dans a²+b²=16

sinon
10ab = 9(a+b)
100a²b² = 81(a²+b²+2ab)
pose ab=X
100X² = 81(16+2X)
100X² - 162X - 1296 = 0
(2X-9)(50X+144) = 0
A toi de finir 

En fait le 10ab = 9(a+b) je l'ai déjà..
J'ai fait Thalès et j'obtient à la fin:
(ab) -0.9 (a+b) = 0
Donc j'ai la même ligne que celleque vous avez mis en premier mais euh je ne comprend pas ce que vous avez fait de la première ligneà la deuxième...
Euh ouais je vois tout ça mais après à la fin je me retrouve avec un produit ab mais moi c'est a et b que je cherche...
Tout à l'heure sur un autre site j'avais trouvé une solution qui consistait à trover que (a+b)² -2(ab)=16 mais le problème c'est que je ne trouve pas comment on fait pour arriver à ça...
Et merci aussi!!!
tu as trouvé ab , c'est parfait
donc tu peux déduire a+b = 10ab/9
tu as donc a+b=S et ab=P => ainsi a et b sont solutions de x²-Sx+P=0
A toi

Euh je crois enfin avoir fini après avoir tenté énormément de choses mais à la fin je trouve des résultats pas piles du tout mais c'est quand même cohérent du point de vue de la figure mais le problème c'est que j'ai deux solutions pour a donc 2 aussi pour b...
Parce que quand j'ai fait le delta pour trouver a j'ai 7 en ayant pour ab=4.5 et a+b=5
Je ne sais pas trop si j'a bon à ça...
Merci
de (2X-9)(50X+144) = 0 tu tires la seule solution positive pour X = ab = 9/2 (a et b étant des longueurs, ab donc X doit être positif )
ainsi ab=9/2
de a+b = 10ab/9 tu tires a+b = 5
ainsi a et b sont solutions de x² - 5x +9/2 = 0
D = (-5)² - 18 = 7
a= (5 - V7)/2 et b = (5 + V7)/2
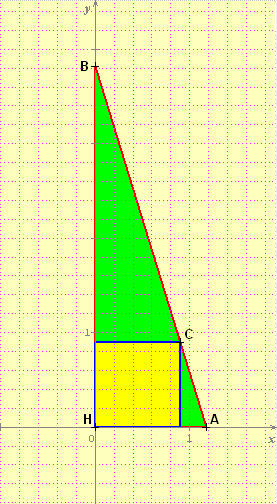
Traité ainsi c'était bien un exo de 1° 

Okay mercri!!!! C'est ce que j'avais trouvé hier soir mais après j'avais remplacé les solutions dans a+b=5...
Merci beaucoup pour vos indications...
Uhm oui un exo de première...


