Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première SuitesTopics traitant de suites [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

problème de 1e S : Barycentre + Suites

Posté par
Sirene 16-05-10 à 23:14

Bonjour à tous,

J'ai actuellement un DNS de Mathématiques à réaliser.
L'un des exercices de ce DNS porte sur un problème de Suites (variations ; limites ; ...).

En voici l'énoncé :


** Partie A

Etant donné deux points A0 et B0 d'une droite, on appelle :

A1 le milieu du segment [A0B0] et B1 le barycentre du système pondéré  {(A0;1),(B0;2)}

An+1 le milieu du segment [AnBn] et Bn+1 le barycentre du système pondéré {(An;1),(Bn;2)}


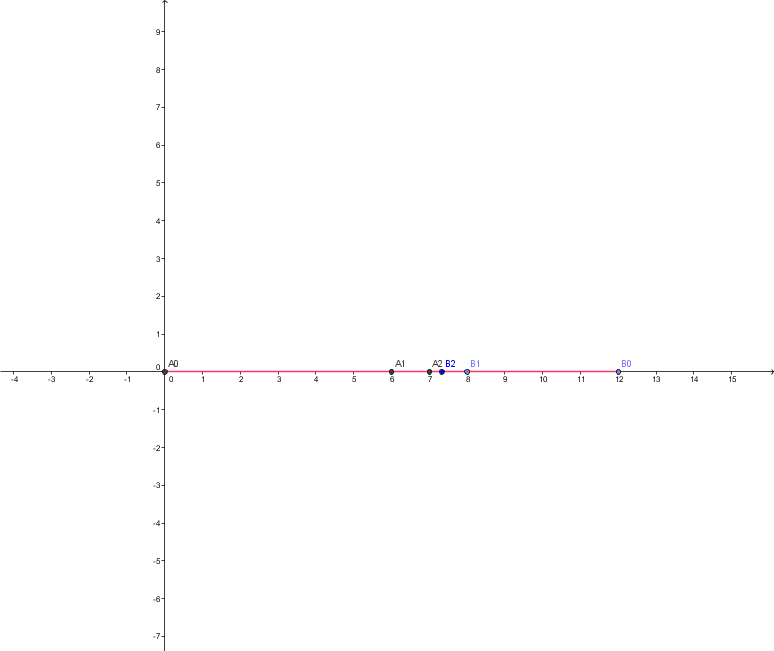
1.     a.  Placer les points A1, B1, A2 et B2 pour A0B0 = 12 cm.
        b.  Quelle conjecture peut-on faire sur les points An et Bn lorsque n devient "très grand" ?

2.     On munit la droit (A0B0) du repère (A0 ;) et = 3$ \frac{1}{12} \vec{2$ A_0 B_0}
        Soit un et vn les abscisses des points respectives de An et Bn.
        Justifier que pour tout entier naturel n non nul,   un+1 = \frac{3$ u_n + v_n}{2}   et   vn+1 = \frac{3$ u_n + 2v_n}{3}

** Partie B

On considère les suites (un) et (vn) définies sur l'ensemble des entiers naturels par :
u0 = 0  ;  v0 = 12  ;  un+1 = \frac{3$ u_n + v_n}{2}  ;  vn+1 = \frac{3$ u_n + 2v_n}{3}

1.     Démontrer que la suite (wn) définie par wn = vn - un est une suite géométrique convergente et que tous ses termes sont positifs.
2.     Démontrer que la suite (un) est croissante puis que la suite (vn) est décroissante.
3.     Déduire des questions précédentes que les suites (un) et (vn) sont convergentes et ont la même limite.
4.     Démontrer que la suite (tn) définie par tn = 2un + 3vn est constante.

** Partie C

Déduire des résultats précédents la limite des points An et Bn lorsque n tend vers +\infty

Posté par
Yzzre : problème de 1e S : Barycentre + Suites 16-05-10 à 23:25

Salut Sirène,
As-tu fait la partie A?
On peut se lancer sur la B si tu veux.
(PS: j'ai complété le boulot de pppa sur ton autre exo)

Posté par
pppare : problème de 1e S : Barycentre + Suites 16-05-10 à 23:44

Citation :
(PS: j'ai complété le boulot de pppa sur ton autre exo)


>> Oh merci Géraud, ça me faisasit peine pr Sirène de le laisser en plan, surtt qu'il prend la peine de donner des énoncés bien propres..

mes meilleurs sentiments à vous deux..

Posté par
Sirenere : problème de 1e S : Barycentre + Suites 18-05-10 à 15:56

Bonjour !

Non mais ce n'est pas grave pppa, le principal a été fait, il ne manquait que 2-3 petites questions !
Sachant que Yzz a terminé, vous vous êtes parfaitement complété .

Sinon pour vous répondre Yzz, je n'ai fait aucune partie .
Je maîtrise assez mal le Barycentre du coup la partie A relative à ce chapitre m'est complexe.
De plus concernant la Partie B sur les suites, ce n'est pas un exercice que j'ai l'habitude de réaliser en classe. Cette partie est plus dédiée à la "recherche" d'où la difficulté qui s'accentue.. .

Voilà.
En espérant que vous pourriez m'aider par la suite Yzz et pppa.

Cordialement

Posté par
Sirenere : problème de 1e S : Barycentre + Suites 20-05-10 à 18:37

Ne m'oubliez pas, c'est pour bientôt !
C'est votre dernière contribution pour moi en +.
Après celui-là, je n'ai pu d'exercices à vous proposer.
Encore un petit effort...

Cordialement

Posté par
pppare : problème de 1e S : Barycentre + Suites 21-05-10 à 18:31

Bonsoir Sirène

Q1 :

A1 est le milieu de [A0;B0]

B1 est le bct de {(A0;1);(B0;2)}

dc [A0;B1] a une mesure double de [B1;B0]
pr avoir la relation caractéristique du bct de 2 pts pondérés.

2.\vec{B_1B_0}+1.\vec{B_1A_0}=\vec{0}

An est le milieu de [An-1;Bn-1]

Bn est le bct de {(An-1;1);(Bn-1;2)}

dc [An-1;Bn] a une mesure double de [Bn;Bn-1]
pr avoir la relation caractéristique du bct de 2 pts pondérés.

2.\vec{B_nB_{n-1}}+1.\vec{B_nA_{n-1}}=\vec{0}

Conjecture : pr n très grand, An et Bn tendent à être confondus.

problème de 1e S : Barycentre + Suites

Posté par
pppare : problème de 1e S : Barycentre + Suites 21-05-10 à 18:54

Pr la fin de la partie A, si tu es en 1èer (en France) je ne pense pas que tu aies appris le raisonnement par récurrence adapté à ce genre de démonstrations.

Je vais m'en inspirer pr répondre à la question

n*, un est l'abscisse du milieu de [An-1;Bn-1]
An-1 a pr abscisse un-1
Bn-1 a pr abscisse vn-1
Dc u_n=\frac{u_{n-1}+v_{n-1}}{2}


vn est l'abscisse de Bn, bct de {(An-1;1);(Bn-1;2)} ; compte tenu de la relation ds mon premier message , on a :

2.(v_{n-1}-v_n)+(u_{n-1}-v_n)=0

2v_{n-1}-2v_n+u_{n-1}-v_n=0

3v_{n} = 2.v_{n-1}+u_{n-1}

v_{n} = \frac{u_{n-1}+2.v_{n-1}}{3}

Tu remplaces n par n+1 et la démonstration tient la route.

Posté par
Sirenere : problème de 1e S : Barycentre + Suites 25-05-10 à 16:27

Bonsoir pppa,

Pourriez-vous terminer le travail du moins finir une autre partie svp ? Car le DNS est pour demain..
Je l'avais pourtant posté il y a + d'une semaine.

Cordialement

Posté par
pppare : problème de 1e S : Barycentre + Suites 25-05-10 à 18:36

bonjour

On pose 3$ w_n=v_n-u_n=\frac{v_{n-1}-u_{n-1}}{6} (fais les calculs)

soit 3$ w_n=\frac{1}{6}\times w_{n-1} et

3$ \frac{w_n}{w_{n-1}}=\frac{1}{6}

Le rapport de 2 termes consécutifs de la suite (wn) étant constant, on en déduit que (wn) est une suite géométrique, de premier terme w0=12 et de raison 1/6.

Pr n=0, on a w0=12, soit w0>0
Soit p* ; on suppose wp>0. On a :
wp+1=(1/6)*wp, soit wp+1>0
Conclusion : n, wn>0.

Par ailleurs : 3$\lim_{n\to +\infty}(w_n)=0^+
(wn) est dc une suite décroissante (vérifie facilement que pr tt n, wn+1<wn), et MINOREE par 0. On applique alors le tm selon lequel  tte suite de réels décroissante et minorée est convergente, ce qui achève la démonstration de la Q1.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !