Inscription / Connexion Nouveau Sujet
Problème de maths sur les fonctions
Bonjour,
J?ai un devoir maison de maths à rendre pour demain et je bloque complètement sur un exercice...
Voila l?énoncé :
1) p est la fonction definie sur ]0 ; +l?infini[ par p(x)=x+1/x
a) étudier les variations de la fonction p. J?ai donc trouvé la dérivée p?(x)=(x^2-1)/x^2 puis étudié le signe de p?(x) avec comme racines 0 et 1 sur l?intervalle cité plus haut. J?ai donc trouvé le tableau de variation avec la fonction p decroissante sur ]0;1[ avec p(1)=2 et croissant sur ]1;+ l?infini[.
b) demontrer que le minimum de p sur ]0;+l?infini[ est egal à 2.
J?ai dit que p?(x) s?annule et change de signe pour x=1 donc il y a un extremum local. Donc f(1)=2 minimum sur l?intervalle ]0;+l?infini[.
2) Sur la figure ci dessous C est la courbe representative de la fonction f definie sur ]0;+l?infini[ par f(x)=1/x. À partir d?un point B de la courbe C on construit un rectangle OMNA avec M point de l?axe des abcisses et A point de l?axe des ordonnées.
Determiner les dimentions du rectangle OMNA de périmètre minimal
Je bloque donc complètement sur cette question :/
***Image redressée et recadrée sur la figure***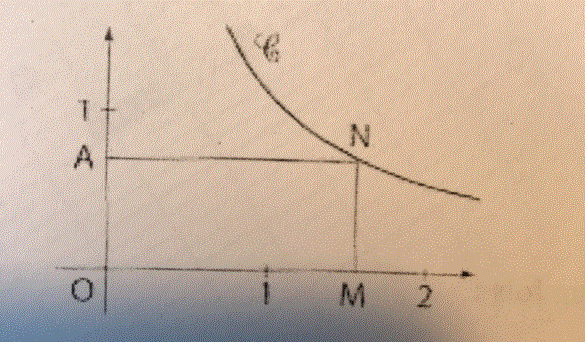
Bonjour
quelques problèmes de rédaction dans la partie 1
la dérivée s'annule uniquement en 1 en 0 la fonction n'est pas définie et donc non dérivable
deux erreurs la première la fonction s'appelle
et la seconde ce n'est pas une conséquence de ce qui précède
question 2 un reste de la photo le point ne s'appelle pas B mais N
quelles sont les coordonnées de N ? Quelle est l'aire du rectangle ?
Merci pour votre réponse,
Oui en effet je me suis mal exprimée j'ai bien mis que la fonction n'etais pas definie en 0 dans mon tableau de signe et de variations.
Par rapport aux coordonnées de N je sais juste que ses cordonnés sont (M;A ) avec M compris entre 1 et 2 et a compris entre 0 et 1. L'aire du rectangle est donc AN*NM mais aucune informations dessus non plus...
quelles sont les coordonnées d'un point d'une courbe ?
dans la partie 1 comment avez-vous trouvé 2 ? les coordonnées du minimum sont .
vous avez un point N qui appartient à la courbe d'abscisse
quelle est alors son ordonnée ?
Dans la partie 1 les coordonnées du minimum sont (1;2) car p(1)=1+1/1=2
Donc pour le point N son ordonnée est f(x)=1/x et donc dans ce cas précis f(M)=1/M.
Mais là ou je ne comprend pas c'est que dans la première partie j'ai trouvé un minimum pour x=1 mais ici si je dérive f(x) j'ai donc f'(x)=-1/x^2. J'etudire ensuite le signe de f'(x) avec d'une part -1<0 et x^2=0 donc x=0 sauf que f(x) n'est pas deifinie en 0
Je ne sais pas si j'ai le droit mais je vous mets en photo le tableau de signes/variations que j'ai réalisé.
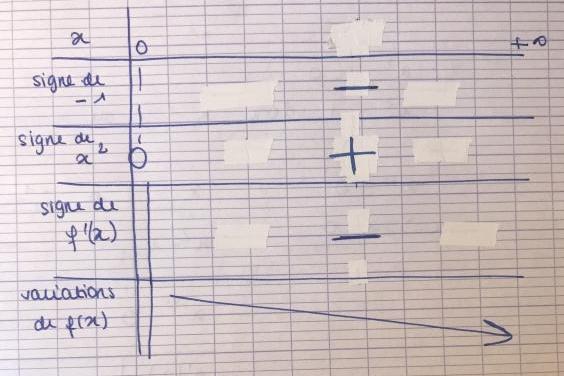
un tableau oui
voir les variations de en principe non et en plus c'est de
qu'il s'agit
mais vous ne répondez pas à ma question je veux les coordonnées de N
désolé je n'avais pas vu le message précédent
les coordonnées de N sont
M est un point on n'applique pas à un point mais à un réel
ensuite il faudrait calculer le périmètre et icelui vaut où
est la fonction de la partie 1
Pourquoi étudier la fonction inverse ? on sait qu'elle est décroissante sur ]0~;~+\infty[
Aaaah oui d'accord merci beaucoup ! Oui je ne sais pas pourquoi j'ai commencé à etudier la fonction inverse. Donc par rapport à la justification puis-je simplement dire que les variations de p(x) et de 2p(x) sont les mêmes car multiplier par 2 ne change pas le sens de variations car 2 est une nombre positif ? Ou dois-je deriver 2x+(2/x), refaire le tableau de variations etc ? Donc on aura 2p(1)=4 donc N(4;2) ?
non il n'est pas besoin de refaire la première partie
le périmètre du rectangle est minimal lorsque et celui ci vaut 4
les coordonnées du point N rendant minimal le périmètre sont



