Inscription / Connexion Nouveau Sujet
problème de régression
bonjour pouvez vous m'aider pour ce problème :
En physique nucléaire, le nombre de nucléons constituant le noyau atomique est appelé nombre de masse et il est noté A. S'il est appelé ainsi c'est que l'essentiel de la masse atomique est contenue dans le noyau. Comme des isotopes ont un nombre de nucléons différents ( même nombre de protons mais nombre de neutrons différents) leurs masses sont également différentes (par exemple l'oxygène 16 a une masse de 15,9949 uma et l'oxygène 18 a une masse de 17,9992 uma). Les masses atomiques sont très petites, c'est pour cette raison qu'elles sont généralement exprimées en unité de masse atomique (uma). L'uma est définie comme étant la douzième partie de la masse du carbone 12,1 uma = 1,660538 10-27.
10-27.
Théoriquement, on peut "construire" des noyau avec n'importe quelle constitution. Cependant, certaines configurations sont instables et se désintègrent très rapidement. On ne peut donc pas mesurer leur masse. Par contre, conaissant les masses de certains isotopes stables du même élément on peut essayer de les estimer.
Considérons le cas du kripton (Kr). On souhaite connaître la masse du kripton 85. calculez cette masse avec la méthode des moindres carrés en utilisant le tableau des masses isotopiques des noyaux stables.
Vérifiez la corrélation de ces données pour discuter la pertinence de votre solution.
| Nombre de masse A | 86 | 84 | 83 | 82 | 80 | 78 |
| Masse (uma) | 85,91 | 83,91 | 82,91 | 81,91 | 79,92 | 77,92 |
merci de votre aide

Bonjour,
la première chose à faire est de porter dans un repère orthonormé (avec des unités bien choisies, pour qu'on y voit quelque chose):
les points de coordonnées (xi; yi) où xi représente le nombre de masse et yi le masse associée.
Evidemment, tu constateras que les points ne sont pas alignés. Néanmoins tu peux te dire que ces couple (xi;yi) sont très proches d'être sur une droite, donc d'obéir à une loi du type f(x) = ax+b
La droite de régression linéaire par la méthode des moindre carré te permet donc de trouver les coefficients a et b de telle sorte que l'on minimise la valeurs  (xi - f(xi)2
(xi - f(xi)2
ces coefficients sont donnés par:
a = [E(XY)-E(X)E(Y)]/V(X) et b = E(Y)-aE(X)
avec E(XY) = (1/6)[(86*85,91)+(84*83,91)+(83*82,91)+ (82*81,91)+(80*79,92)+(78*77,92)]
E(X) = (1/6)(86+84+83+82+80+78)
E(Y) = (1/6)(85,91+83,91+82,91+81,91+79,92+77,92)
V(X) = (86-E(X))2+(84-E(X))2+...+(78-E(X))2
calcule donc:
a =...
b = ...
tu obtiens l'équation de la droite de régression linéaire qui approxime "au mieux suivant la méthode des moindre carré" la loi qui régit yi en fonction de xi
donc:
pour x = 85 tu trouveras y en calculant y = ax+b = a(85) + b
bonjour,
voici les calcul que je fais:
equation de la droite
pour trouver m : 


= 1,04
pour trouver p : 


Petite correction dans mon post de 17h06: il manque (1/6) en fecteur dans la formule de la variance.
Donc:
V(X) = (1/6)[(86-E(X))2+(84-E(X))2+...+(78-E(X))2]
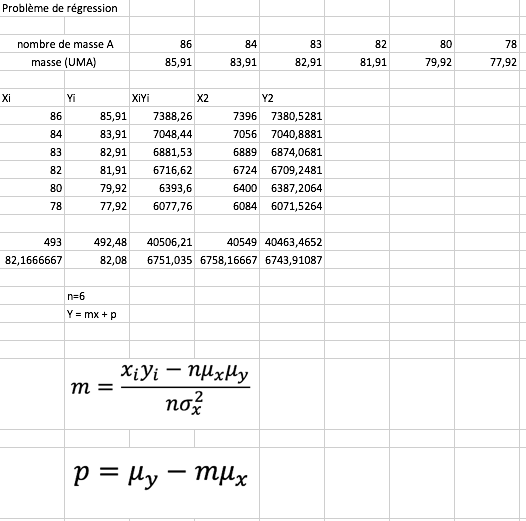
Avec un tableur Excel:
je trouve pour y = mx + p
m = 0.998449
p = 0.040776
Ce qui me semble logique puisqu'au regard des valeurs de x et de y de départ, on s'attend à trouver une droite de régression linéaire proche de y = x donc m proche de 1 et p proche de 0.
Donc comme y = mx + p = 0.998449x + 0.040776
Alors la masse du Krypton 85 est obtenue pour x = 85
y = 0.998449(85) + 0.040776 = 84,90893878 uma  84.91 uma
84.91 uma
tes formule pour m et p étant les mêmes que les miennes, tu fais des erreurs de calculs!
mais tu as une mauvaise rédaction:
m = [ (xiyi)-nµxµy]/n
(xiyi)-nµxµy]/n x2
x2
p = µy-mµx
Ton erreur de calcul est une erreur d'arrondi:
tu dois prendre ta vraie valeur µx et ne pas l'arrondir à 82.17


