Inscription / Connexion Nouveau Sujet
Problème de synthèse dérivation
Bonsoir, en cette fin de vacance je retravaille les chapitres abordés durant l'année passée.J'ai donc trouvé un exercice qui porte sur la dérivation mais je bloque,j'aurai donc besoin de votre aide si possible.Voici l'énoncé:
Soit f la fonction la fonction auxiliaire: g est définie sur ℝ par g(x)= x^4+2x^3-2x+1
1) Etude d'une fonction auxiliaire: g est définie sur ℝ par g(x)=2x^3+3x^2-1
a)calculer g'(x)
b)étudier le signe de g'(x) et en déduire les variations de g
c) calculer g(1/2) et en déduire le signe de g(x) sur ℝ
2)Etude des variations de f
a) montrer que f'(x)= 2g(x)
b) en déduire le signe de f'(x) puis les variations de f sur ℝ
3)Précisez les points où la tangente est horizontale.
4)Déterminer une équation de la tangente à la courbe représentative de f au point d'abscisse 0.
5) Dans un repère orthonormé d'unité 3 cm placer les tangentes horizontales, la tangente en 0 puis tracer la courbe
Voici ci-dessous le travail que j'ai fait avant d'être bloqué :
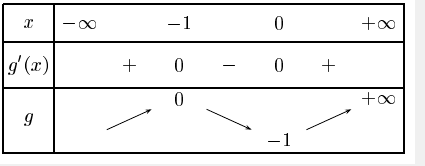
1) a) g'(x)=6x^2+6x
b) g(-3)=-28 g(0)=-1 j'ai fait un tableau
c)g(1/2)=0
2) f'(x)= 4x^3+6^2-2 et 2g(x)= 2(2x^3+3x^2-1)
=4x^3+6^2-2
Je vous remercie par avance de l'aide que vous pourrez m'apporter.
Bonjour
Revoir le début de l'énoncé : fonction f non définie et fonction g définie de 2 façons différentes.
Même si on peut deviner ce c'est pas à nous de faire ces divinations.
Bonsoir,
1)b) La réponse n'est pas claire, et pourquoi calculer g(-3)?
Si cette question n'est pas clairement résolue, il sera difficile de traiter la 1) c) puis la suite
Bonsoir, pour la question 1)b) je me suis trompée lorsque l'on cherche les racines de 6x^2+6x on trouve 0 et -1. De ce faite g(1/2) se trouve sur [0;+∞[ qui est croissant le signe est donc +.
non car là vous donnez l'ensemble sur lequel est positive
on vous demande le signe de ce n'est pas pour rien que l'on vous a fait calculer
si
si
si
d'accord vous auriez pu compléter si ou
ensuite signe de et sens de variation de
cela ne devrait pas poser de problèmes
3 ? 4 ?