Inscription / Connexion Nouveau Sujet
problème de synthèse trigonométrie
Bonjour à tous. Je sollicite votre aide pour m'aider à résoudre l'exercice suivant
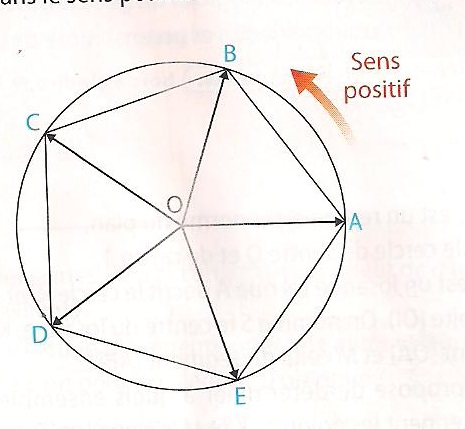
ABCDE est un pentagone régulier direct inscrit dans un cercle de centre O : les points A, B, C, D et E sont situés sur le cercle dans cet ordre et dans le sens positif.
1)a) Déterminer les mesures en radians des angles ABO et BOD
b) En déduire les mesures principales en radians des angles (BO,BA), (DO,OB) et (DO,AB)
2) Démontrer qu'une mesure en radians de (DO,EC)est 
/2
3)a) Déduire des questions précédentes que les vecteurs OA+OB et OC+OE sont colinéaires à OD
b) En déduire que 0A+OB+OD+OC+OE est colinéaire à OD
4) Démontrer que les vecteurs OB+OC, OD+OA, OA+OB+OD+OC+OE sont colinéaires à OE
5) Déduire des questions précédentes OA+OB+OD+OC+OE= 0
Merci d'avance pour votre je n'ai pas encore vu la leçon des angles orientés de vecteurs en cours.
Bonjour, et tu en es où ?
tu peux trouver facilement AOB (le tour complet fait 2 et il est découpé en 6 angles égaux) puis OAB est isocèle donc si tu as l'angle au sommet, tu peux trouver la valeur des angles à la base, etc ...
en fait c'est un chapitre que je n'ai pas encore abordé en cours Peux tu m'expliquer la méthode pr la question 1 stp?
1) j'ai rectifié mes erreurs
ABO=360/5 = 72°
*72=180
=72/180 = 2/5 rad
BOD=2*72 =144°
*144=180
=144/180 = 4/5 rad
je ne comprends pas bien tes calculs :
Reprenons :
AOB est le sixième du tour complet donc AOB= 2/6 = /3
Le triangle AOB a donc un angle au sommet égal à /3, si les deux autres valent x alors 2x+/3= donc 2x=2/3 
x=/3 donc en fait AOB est équilatéral.
DEOC est un losange (les 4 cotés sont égaux) donc les diagonales se coupent à angle droit et donc (DO,EC)=/2
Et tu n'essayes jamais de trouver par toi même ?
OA+OB=-2OD et OC+OE=OD donc 0A+OB+OD+OC+OE=-2OD+OD+OD=0
En fait j'avais oublié la leçon des vecteurs, ce n'était pas frais dans ma tête donc je l'ai relu. Je ne suis pas ici pour que vous fassiez mon devoir. Je souhaite travailler 
Annuler
connectez vous