Inscription / Connexion Nouveau Sujet
probleme derivation
Bonsoir,
J'ai absolument besoin d'aide, je dois rendre mon devoir *****
Je bloque sur la deuxième question du cas particulier de brook.
J'ai trouvé une équation de la tangente
y= -4x+5
et j'ai essayé de faire correspondre les deux courbes en les egalisant
-4x+5=1+(1/x)
mais je n'arrive pas a la proposition de la question 2.
Please help ....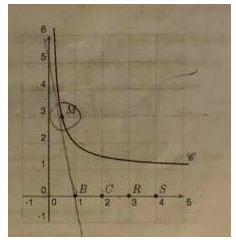
*image recadrée conformément à ![]() Sujet ancien- ne plus donner ce lien-merci*
Sujet ancien- ne plus donner ce lien-merci*
*malou>la gestion du temps est ton problème, tout dépendra de ton investissement sur le sujet*
* si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
Desolée .
Bien j'ai trouvé une tangente au point M
y= -4x+5
On me demande de prouver que
Xo^2 + 2Xo -1 = 0
en sachant que le point M a pour coordonnées (Xo, f(Xo) )
Merci
Avant de disparaître, je te signale que ta trouvaille est fausse :
J'ai trouvé une équation de la tangente
y= -4x+5
Adieu

Bonsoir,
comme déjà demandé,
si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
On souhaite trouver en quels points de sa trajectoire le coco news doit lâcher les journaux pour que ceux-ci atteignent les quartes cibles.
Cas général on note X0 l'abscisse du point de largage du journal.
ton énoncé n'est certainement pas complet!
la courbe C on en dit quoi?
je bloque sur la deuxième question du cas particulier de brook??
question 2?
Ta deuxième proposition d'équation est tout aussi fausse que la première...
Ce n'est pas avec des petits bouts d'énoncé qu'on va pouvoir t'aider.
La règle est :
Vous devez RECOPIER L' ÉNONCÉ sur le forum (ne pas raconter l'énoncé, on recopie à partir du 1er mot jusqu'à au moins la question qui pose problème...)
Le bla-bla du départ est sans intérêt mathématique.
Ton énoncé commence à :
La COCO news / mouette factrice est représentée par le point M et sa trajectoire a pour équation y = 1 + (1/x) ....
Le point B représente l'ami BROOK.
Tu as déjà recopié un peu de la suite :
On souhaite trouver en quels points de sa trajectoire le coco news doit lâcher les journaux pour que ceux-ci atteignent les quatres cibles.
Cas général on note X0 l'abscisse du point de largage du journal.
Fais l'effort demandé de compléter l'énoncé (les questions 1 et 2 ?)
Puis dis nous ce que tu as répondu à ces 2 questions !
(on réglera le cas particulier de Brook après... si tu en as encore envie.)
A toi de faire et de dire.



