Inscription / Connexion Nouveau Sujet
Problème exercice
Bonjour à toutes et à tous ,
J'ai de très gros problème avec cet exercice :
On donne ci-contre la courbe représentative de la fonction f définie sur [ -(4/5) ; + ? [ par f(x)=?(5x+4). A est le point de la courbe d'abscisse 1 , B celui d'abscisse 0, les tangentes en A et en B sont dessinées .
1 . Lire le nombre dérivé de la fonction f en 1 , en 0.
2. En vous inspirant de la démonstration de la dérivabilité de la fonction racine carrée en a>0 déterminer f'(1). 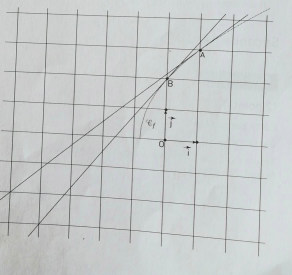
***image recadrée***
Bonjour,
question1 : il n'y a qu'à lire en observant des points de la tangente qui sont à l'oeil exactement sur des points du quadrillage.
question 2 : "en s'inspirant" ... peut être faudrait il revoir en détail cette fameuse démonstration là (cours) ...
un truc sur la simplification et la limite de (f(x)-f(1))/(x-1) quand x → 1
tu devrais y voir (dans cette démonstration du cours) apparaitre l'utilisation d'une "quantité conjuguée" pour réussir à mettre x-1 en facteur au numérateur
mathafoumathafou
Bonjour
Donc pour la question 1 :
f'(1) = 1
f'(0) = 0 ? ( c'est pour celle la que je n'y arrive pas)
En revanche je ne comprends pas la 2
Bonjour,
merci à malou pour le recadrage de l'image
Ocem33, tu dois étudier les cours AVANT de poster tes exercices
(le diplôme n'est pas envoyé par la poste gratuitement)
place 2 nouveaux points, avec des coordonnées entières :
A' sur la tangente passant par A
B' sur la tangente passant par B
compte les petits carreaux de bas en haut, et de gauche à droite
permettant de passer de A' à A, ( et de B' à B)
Barney
Ok merci,
Donc pour la 1 :
f'(1)= 5/6
f'(0)= 5/4
Est-ce bon ?
(Je ne comprends toujours pas la 2)
oui, c'est exact; entrainement indispensable
sur quel intervalle la fonction racine carrée est définie et continue ?
sur quel intervalle la fonction racine carrée est elle dérivable ?
Quelle est la dérivée de la fonction racine carrée ?
l'énoncé exige de s'inspirer de la preuve de dérivabilité (et donc du calcul de la dérivée) de racine de x
c'est à dire exactement comme j'ai dit :
en effectuant et discutant explicitement ce calcul là
et pas du tout sur un calcul de fonction composée
donc LIRE LE COURS !!
sur comment a été démontrée et calculée la dérivée de
mathafou
Vous savez je ne suis pas bonne en math j'ai beaucoup de difficultés et je n'arrive pas a comprendre surtout ici même avec tous ces éléments je ne comprends pas😔
Je dois finir ceci aujourd'hui ou demain au plus tard mais la je suis totalement bloquée
apprendre son cours est indispensable
voire encore plus indispensable : savoir fouiller dedans , y compris dans ce qui a été "fait en cours"
ensuite les maths cela s'apparente énormément à jouer au LEGO en assemblant des briques que l'on recopie à gauche à droite et que l'on modifie en appliquant les règles de calculs élémentaires apprises au collège sur les développements etc
c'est tout
et refuser d'écrire la moindre ligne (qui ait un sens) ne va pas arranger les choses bien au contraire !
dans le mot "exercice" il y a la notion de s'exercer, donc de faire et refaire encore et encore les mêmes "gestes" de recopier, développer etc etc.
donc
définition de la notion de dérivée (cours à apprendre "par coeur")
1. Définition ![]() Cours sur les dérivées et la dérivation
Cours sur les dérivées et la dérivation
Soit
On dit que
Cette limite est appelée nombre dérivé en
traduction directe et immédiate ici pour étudier la dérivée en
étudier le rapport
ou ce qui revient au même
et bien entendu la première chose à faire et elle est absolument indispensable
est d'écrire ce rapport avec la fonction f(x) ecrite explicitement et de par sa définition de l'énoncé :
comment pourrait on aller plus loin si on ne fait pas au minimum ça ???????
ensuite on va essayer d'améliorer les choses parce que sans précaution particulière le numérateur tend vers 0 et le dénominateur aussi et 0/0 n'a aucun sens.
donc il faut trouver un moyen de simplifier....
et l'énoncé de l'exercice affirme que la technique pour faire ça a été vue (en cours) à propos d'une autre fonction "du même genre"
et il demande de s'inspirer de ce qui a été fait à ce moment
évidement si aucune note n'a été prise à ce moment tu ne risques pas de t'inspirer de quoi que ce soit ...
mais on verra bien plus tard
(vu que pour l'instant tu n'as strictement rien écrit du tout ...)
non.
ce n'est pas du tout ce qui est demandé
(en plus c'est faux : vu que tu devrais retrouver le résultat de la question 1)
ce qui est demandé explicitement c'est :
En vous inspirant de la démonstration de la dérivabilité de la fonction racine carrée en a>0 déterminer f'(1).
c'est à dire explicitement ce que je me tue à répéter
écrire explicitemen (je te le fais, na, bouché)
on veut étudier (explicitement) la limite si elle existe de :
quand x tend vers 1.
etc...
et pour cela tu dois t'inspirer (même technique mais calculs différents) du calcul qui a été fait en cours sur l'étude de la limite de
je te fais le début (sur l'exemple de
on reconnait au numérateur un (A-B)(A+B) donc identité remarquable etc
et au final la simplification par (x-a)
ce qui va permettre de faire tendre x vers a sans avoir besoin diviser par 0 !
il faut faire pareil mais avec au lieu de
ne pas oublier la question de Barney
sur quel intervalle la fonction racine carrée est définie et continue ?
(ça commence comme ça en fait avant même de faire quelque calcul que ce soit)
n'importe quoi ... (aucun rapport avec quoi que ce soit)
toujours cette histoire de briques qu'on remplace par copier coller
c'est du calcul quasiment mécanique
se tromper, à ce stade de tes erreurs, c'est juste parce qu'on n'a pas fait attention en recopiant des morceaux de la formule, qu'on en a oublié des bouts etc
s'inspirer de
pour faire pareil, avec la fonction de l'énoncé et avec a = 1 c'est écrire que
(remplacement texte à texte de briques que l'on copie-colle)
pour simplifier l'écriture on a calculé la valeur numérique de
maintenant comme j'ai dit
il faut reconnaltre une identité remarquable (A-B)(A+B) dans
(A-B)(A+B) = A² - B² donc ... (encore des briques à remplacer textuellement ...)


