Inscription / Connexion Nouveau Sujet
Probléme- Loi Binomiale
Bonjour,
je suis en première E.S et j'ai un problème portant sur de la loi binomiale qui me pose réellement... problème.
Une urne contient 10 boules rouges et 10 boules bleues. On tire n boules successivement et avec remise, avec n entier supérieur ou égal à 2.
On considère les évènements suivants : A:"on obtient des boules des deux couleurs" et B:"on obtient au plus une boule rouge".
1. Calculer en fonction de n la probabilité que toutes les boules tirées soient de la même couleur, et en déduire p(A)
2. Calculer la probabilité de B en fonction de n
3. Comparer p(A) et p(B) lorsque l'on tire deux boules successivement et avec remise
4. On veut comparer P(A) et P(B)suivant les valeurs de n .
a. Monter que comparer P(A)et P(B) revient à comparer 2^n -n-3 à 0
b. Soit la suite (un) définie pour tout entier naturel n, par: un= 2^n -n-3
Monter que cette suite est croissante et en déduire que pour n supérieur ou égal 3: un strictement supérieur à 0.
Mon problème arrive dés les premières questions je n'arrive pas à savoir si le résultat semble tenir la route 
Pour le petit un je trouve P(A) = 1-( (1/4 ^n) * 2
pour le petit deux je trouve P(B) = 1/2 * 1/2^n-1
Merci de me confirmer si le début est juste et éventuellement me donner des pistes pour la suite 
Bonsoir choupazou,
1. Pourquoi as-tu utilisé la valeur 1/4 ?
La probabilité d'obtenir une boule rouge ( ou une bleue ) est de 1/2
2. Si X est le nombre de boules rouges , il suffit de calculer p(X=0) + p(X=1) avec B(n;1/2)
Bonsoir, d'abord merci pour votre aide
si j'ai mis 1/4 c'est parce que dans mon arbre j'ai multiplié ( 1/2 * 1/2 ce qui fait 1/4)
Du coup je ne sais pas ce qui est juste 
Si tu fais un arbre représentant n tirages ( peut-être un peu plus grand que ce que tu as utilisé ), la branche "uniquement des boules rouges " donne une probabilité de (1/2)n
Idem pour la branche "uniquement des boules bleues "
Ainsi pour p(A) on aura 1 - 2 * (1/2)n
Pour p(B) , essaie de t'inspirer de l'arbre joint ; il n'y a que les branches en trait épais qui conviennent
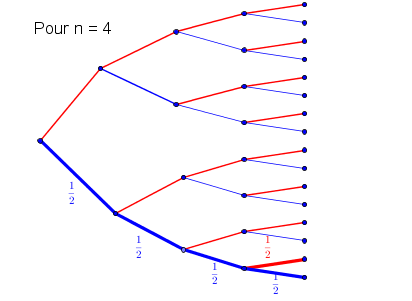
Je crois avoir mieux compris, je me suis trompé au niveau des branches de mon arbre( j'ai mis que la probabilité était 1/4)
je vais essayé de me débrouiller pour la suite.
En tout cas encore merci pour votre aide, car je faisais fausse route.


