Bonjour,

on ne voit pas ton calcul. Pour exprimer une fraction, utilise les parenthèses et le /

Bonjour,

Et... bon courage !

La base des logarithmes népériens est notée e
e = 2,718 281 828 ...

Pour cela, prendre la calculette et faire e^x avec x = 1

Pour la loi de Poisson :


est la moyenne de la loi de Poisson, ici = 1,6

e^-1,6 = exp(-1,6) = 0,201 896 518 ... (prendre la calculette !)
k est le nombre de cas auquel on s'intéresse, ici k = 2
k ! = 1 * 2 = 2

P(X = 2) = e^-1,6 * 1,6² / (1 * 2) = 0,258 4...

Bonjour Coll  

Je viens de me replonger dans la Loi de Poisson grâce à Wiki  

Bonjour borneo
La loi des événements rares... vérifiée une des premières fois sur le nombre de morts par ruades de cheval (voilà qui devrait vous intéresser... )

merci beaucoup pour botre aide mais je vous embeterez surement encore très souvant.
Encore merci

Le service d'assistance téléphonique d'un éditeur de logiciel reçoit en moyenne 1 appel par 10 minutes (ou 600 secondes). On étudie la loi de la variable X représentatn le ombre d'appels en 1 heure.
dt=1 seconde    p= 1/600= 0.001666    T=1 heure = 3600 secondes
appels en 1 heure : 0.001666*3600=6

On calcule le probabilité de recevoir :
1) 6 appels en 1 heure : P(X=6) = e[-6]x6[2]/6*1 c'est mon calcul mais je me plante forcément puisque lui il trouve 0.16 comment?
2) Plus de 6 appels : P(X>6)= 1- P(X<=6) il trouve 1-0.6063=0.3937 je ne comprends pas
3) 4 appels au plus P(X<= 4 ) = 0.2851

Merci d'avance pour votre aide

Si vous savez utiliser un tableur c'est le moment...
(et si vous ne savez pas, c'est le moment d'apprendre )



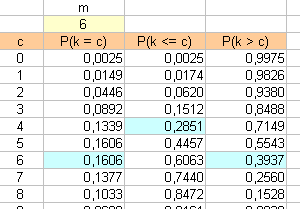
J'ai coloré en bleu les trois cases qui répondent au problème.

P(X=6) = e^-6 * 6⁶ / (1.2.3.4.5.6)

Correction pour la formule donnée à 12 h 34 pour une loi de Poisson de moyenne



et dans le cas particulier k = 2



Excusez-moi

Merci mais pourriez vous me poser les opérations me permettant de trouver le nmbre pour plus de 6 appels et le nombre pour 4 appels au plus?

Je peux écrire les "belles" formules avec de superbes

Regardez bien le tableau
La troisième colonne P(k<=c) fait la somme P(0) + P(1) + P(2) + P(3) + P(4)
et ceci vaut P(X 4)

La quatrième colonne fait simplement 1 - P(X c) = P(X > c)
Et "plus de 6 appels" est bien le contraire de "au plus 6 appels"

D'accord ?

Vous avez raison de poser les questions qui vous tracassent. N'hésitez pas !

D'accord ça j'ai compris mais quand je calcule par exemple P(k=c) =5

Je pose bien P(X=6) = e[-5] * 5[5] / (1.2.3.4.5)
? Si c'est exact ça me donne 0.17546 et vous c'est noté 0.1606 c'est ça que je comprend pas. Et le jour de l'examen je n'aurai pas de tableur donc il faut que je sache les calculer à la main!

C'est bon j'ai compris mon erreur en fait il faut que je calcule:
e[-6] car variable = 6     *
6[5] car variable 6 exposant 5 puisque X =5       /
1*2*3*4*5 car X=5
soit e[-6]*6[5]/(1*2*3*4*5)=0.1606   C'est ça?

Oui, la moyenne est = 6

Donc pour le calcul de X = 5 il faut bien faire :

P(X = 5) = e^-6 * 6⁵ / (1.2.3.4.5)

Donc pour les autres calculs il suffit que je calcul la première colonne et faire des additions et des oustractions pour le reste

Par quel moyen tu arrives à écrire e exposant -6 dans les réponses que tu me donnes (que l'exposant soit eu dessus de e)

Très exactement.

Et cette première colonne ne se calcule pas avec la formule "des livres"

Elle se calcule ainsi :

P(X = 0) = e^-

P(X = 1) = P(X = 0) * ( / 1)

P(X = 2) = P(X = 1) * ( / 2)

P(X = 3) = P(X = 2) * ( / 3)

...

P(X = n) = P(X = n-1) * ( / n)

C'est très facile à démontrer. Essaie et convaincs-toi !

Pour écrire e^-6

Je tape e-6
Je sélectionne -6
Je clique sur le petit bouton x² qui se trouve en bas du cadre d'écriture, au-dessus de "POSTER"
Cela place des balises [sup][/sup] autour de la sélection... et le tour est joué !

merci beaucoup pour ton aide

Je t'en prie.
A une prochaine fois !

Up pour un autre élève qui a ce genre d'exo