Inscription / Connexion Nouveau Sujet
Probléme ouvert
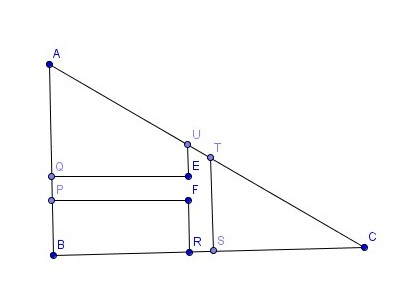
Charlotte posséde un jardin en forme de triangle ABC, rectangle en B, avec BA=30 m et BC= 40m.
Elle y a tracé une allée large de 2m telle que les trois parties restantes (un triangle rectangle, un rectangle et un trapèze rectangle) ont la même aire.
Déterminer les longueurs SG, ST, BR, BP, AQ et UE.
Bonsoir
bonsoir , s il vous plait, merci , c est tellement plus agreable a lire! et ,ça donne envie de repondre !!!
Bonsoir, tu prends des inconnues comme BR=x et BP=y, tu exprimes toutes les autres longueurs en fonction de ces deux là. tu écris que les 3 aires sont égales, ça te donne deux équations qui te permettent de trouver x et y.
Bonsoir !
Glapion : Je ne comprend pas ton système de résolution en prenant des inconnus ( x=BR .. ) , peux-tu m'en dire un peu plus s'il te plaît
Merci d'avance ! 
Exprime toutes le longueurs en fonction de x et y. Par exemple si BP=y, AQ=AB-BP-PQ=30-2-y=28-y
SC=BC- BR -RS= 40-2-x=38-x, etc...
Merci pour ton explication, mais après avoir exprimé toutes les longueurs en fonction de x et y, je n'arrive pas à trouver un moyen de déterminer les longueurs .. Faut-il calculer les aires ? Comment trouver une équation permettant de trouver x et y ?
Merci de ton aide !
Tu ne lis pas les posts, je t'avais dit : tu écris que les 3 aires sont égales, ça te donne deux équations qui te permettent de trouver x et y.
Je te dit ce que j'ai essayer de faire :
BR=x BP=y SC=a ST=s AQ=q UE=m
xy = (a*s)/2 = ((q+m)*x )/2
Là je pense que j'ai les 3 aires qui sont égales, je n'arrive pas à trouver x et y ! Ca fait bientôt 2 semaines que j'y réfléchis, peux tu m'aider un peu plus s'il te plaît, car je dois l'avoir fait pour mercredi ! Merci d'avance ! 
Bon donc on pose x=BR et y=BP
SC=40-x-2=38-x
AQ=30-y-2=28-y
Pour ST il faut faire un peu de Thalès entre les triangles CST et CBA : ST/AB=CS/CB  ST/30=(38-x)/40
ST/30=(38-x)/40  ST=(3/4)(38-x)
ST=(3/4)(38-x)
Pour RU aussi : RU/AB=CR/CB  RU=(3/4)(40-x)
RU=(3/4)(40-x)
EU=RU-2-y=(3/4)(40-x)-2-y
on a maintenant toutes les distances qu'il faut en fonction de x et y.
le rectangle fait xy
le petit trapèze : (AQ+UE)QE/2=(28-y+(3/4)(40-x)-2-y)x/2
le triangle : SC.ST/2 = (3/4)(38-x)(38-x)/2=(3/8)(38-x)²
Et donc nos égalités sont (3/8)(38-x)²=(26-2y+(3/4)(40-x))x/2=xy
l'inégalité de droite peut être simplifiée par x
(26-2y+(3/4)(40-x))/2=y  y=14-3x/16
y=14-3x/16
(3/8)(38-x)²=xy  (3/8)(38-x)²=x(14-3x/16) équation du second degré , moi j'ai trouvé x=16.2 et y~11 à vérifier
(3/8)(38-x)²=x(14-3x/16) équation du second degré , moi j'ai trouvé x=16.2 et y~11 à vérifier
Bonsoir, je suis votre conversation depuis un petit moment, J'aimerais simplement savoir comment as-tu fait ( glapion) pour résoudre :
(26-2y+(3/4)(40-x))/2=y ==> y=14-3x/16
Merci pour ton aide !
comment faire pour mettre en equation 2nd degré ? : (3/8)(38-x)²=xy (3/8)(38-x)²=x(14-3x/16)
Merci pour ce que tu as fait !!
bonjour, quelqu'un pourrait m'expliquer :
"l'inégalité de droite peut être simplifiée par x
(26-2y+(3/4)(40-x))/2=y y=14-3x/16
(3/8)(38-x)²=xy (3/8)(38-x)²=x(14-3x/16) équation du second degré"
je n'arrive pas a trouver l'équation du second degré
Kayna pour trouver l'équation du second degrès il suffit de passé un membre de l'autre coté je m'explique
faire : x(14-3x/16)-(3/8)(38-x)²
et la tu a ta forme du seond degrès.
bonjour ,
x(14-3x/16)-(3/8)(38-x)² je l'ai développer c qui m'a donné -9x/16+85/2x+1083/2
comme équation du second degré mais après mes résultats ne sont pas bon donc je pense que mon équation est fausse
Bonjour à tous,
Moi aussi je suis votre conversation depuis un petit moment, car cet exercice m'a été donné en DM à rendre pour cette semaine.
J'ai trouvé la même réponse que toi kayna mais je reste bloqué.
Je voulais savoir si, après avoir trouvé l'équation -9x²/16+85/2x+1083/2 , faut-il bien calculer delta pour trouver les deux réponses car delta est positif ? on aurait alors x1=... et x2=... Ou peut être faut il faire autre chose ?
Au passage, moi j'ai trouvé que l'équation était égale à -9x²/16+85/2x-1083/2 Peut être ai je fais une erreur de calcul ?
Merci d'avance
Bonsoir tout le monde,
J'ai également cet exercice en DM à rendre pour jeudi (je suis en 1èreS), et après avoir trouvé que y=14-3x/16, je me demande quelle est la marche à suivre.. Résoudre l'équation
(3/8)(38-x)^2 = xy
(3/8)(38-x)^2 = x(14-3x/16)
(3/8)(38-x)^2 - x(14-3x/16) = 0
... ?
Je ne vois pas tellement ou cela mène à part qu'on a une équation du 2nd degré sous la forme canonique, avec a=3/8, alpha=-38 et bêta=-x(14-3x/16) .. si je ne me trompe pas.
Ma foi je comprends pas grand chose ^^' quelqu'un pourrait-il m'éclairer?
Pour répondre à la question précédente,
je pense qu'il faut développer cette équation comme l'a fait kayna, puis ensuite calculer delta qui nous permettrait de trouver les solutions dont la valeur de x, qu'on remplacerait ensuite dans y=14-3x/16...
Mais le problème, c'est que quand je calcule delta, je trouve des solutions assez insolites avec des grands nombres, des racines qui ne se simplifient pas...
En uilisant l'équation que j'ai développé: -9x²/16+85/2x-1083/2, pour delta, je trouve  = 4703/8
= 4703/8
Est ce possible ? ça me semble bizare... parce qu'ensuite, ce n'est plus cohérent.
J'ai calculé delta et je trouve la même valeur que toi.. Ce que je ne comprends pas, c'est l'utilité de calculer les racines, puisqu'il ne peut y avoir qu'une valeur de x et une de y pour lesquelles les aires sont égales..
Oui c'est vrai, je ne vois pas l'utilité non plus. Mais peut être y a-t-il une valeur plus appropriée que l'autre ? A l'aide d'un programme fait sur ma calculatrice pour trouver les solutions d'une équation du second degrès, j'ai trouvé x1 environ égale à 59,33 et x2 environ égale à 16,23 (arrondis au 100 ème).
Peut être peut on faire quelque chose avec ces valeurs ?
Si j'en crois les messages précédents 16,2 serait la valeur de x trouvée en fin d'exercice.. Mais je ne vois pas comment prouver que c'est bien ça! :/
Parce que si je résume, on fait:
(3/8)(38-x)^2 - x(14-3x/16)
=(9/16)x^2-(85/2)x+(1083/2)
on a donc ici une équation du 2nd degré de la forme ax^2+bx+c avec a=9/16, b=-85/2 et c=1083/2
on peut calculer delta = b^2-4ac = 587.875 = 4703/8
on a un résultat positif donc deux solutions à l'équation (9/16)x^2-(85/2)x+(1083/2)=0, qui sont x1=16.23 et x2=59.33
après je ne vois pas comment justifier le choix de la première racine, à part en disant que x ne peut pas prendre la valeur 59.33 puisque x est forcément inférieur a 40 .. Mais peut-être cela est-il suffisant, qu'en pensez-vous?
Ensuite il suffirait de remplacer x par cette valeur pour trouver y, calculer les 3 aires et les valeurs de SC, ST, BR, BP, AQ et UE.
En fait, je suis un peu perdu parce qu'au départ, nous ne faisions pas un système ? Nous avions trouvé que y était égale à 14-3x/16 donc peut être faut il remplacer le x dans y par 16,23.
Mais le problème, c'est que 16,23 est une valeur arrondie ! Donc je pense que ce n'est pas logique et qu'il faut trouver un autre moyen, ou à moins d'avoir la bonne valeur de x correspondant à 16,23.
Mon second problème, c'est que ce 16,23, je l'ai trouvé grâce à un programme de ma calculatrice permettant de trouver les solutions de delta; car à la main, je n'y arrive pas: les racines au dénominateur car racines qui ne se simplifient pas...
Quel problème !
C'est aussi compliqué car je remarque que l'on a pas les mêmes signes pour le développement de l'équation x(14-3x/16)-(3/8)(38-x)²
mmeblois a  9/16)x^2-(85/2)x+(1083/2)
9/16)x^2-(85/2)x+(1083/2)
kayna a : -9x/16+85/2x+1083/2
et moi j'ai : -9x²/16+85/2x-1083/2
Il faudrait peut être se mettre d'accord ^^ non ?
Ok.
Est ce que l'un de vous a réussi à faire le calcul à la main pour trouver les 2 solutions de delta, dont celle égale à 16,23, sans arrondis ?
Ou pensez vous peut être que l'on devrait mettre la valeur arrondie 16,23 pour remplacer le x ?
Sinon, le raisonnement de mmeblois me semble juste.
Qu'en pensez vous ?
(3/8)(38-x)² - x(14-3x/16)
=(3/8)(38²-2*38*x+x²) - 14x+(3/16)x²
=(3/8)(1444-76x+x²) - 14x+(3/16)x²
=1083/2-(57/2)x+(3/8)x² - 14x+(3/16)x²
=(9/16)x²-(85/2)x+1083/2
Sommes-nous d'accord?
Eh bien, comme mmeblois l'a dit précédemment : "il suffirait de remplacer x par cette valeur pour trouver y, calculer les 3 aires et les valeurs de SC, ST, BR, BP, AQ et UE."
La valeur étant x=16,23
On peut toujours essayer et constater si les 3 aires sont égales. On pourra donc, avant cela, calculer les valeurs des différentes longueurs grâce à ce que l'on a déduit au début: par exemple SC= 38-x, AQ= .... etc en remplaçant le x ou le y, à chaque fois, par les valeurs trouvées dans le système précédent. (x=16,23 et y= ... à calculer) puis calculer les 3 aires.
Par contre, les valeurs des longueurs seront arrondies et je pense que si l'on calcule les 3 aires, elles seront donc aussi approximatives: elles seront environ égales.
C'est ça qui est gènant.
Bon, pour ma part, je vous dirai ce qui en est demain, si j'ai avancé ou non.
Bonsoir à tous et merci pour votre aide.
Je tenais à m'assurer que les signes soient bons histoire de ne pas fausser le résultat après tout ce qu'on a fait ça serait quand même dommage ^^'
Kayna et Myss, remplacez x par une valeur entière comme 3 par exemple et calculez (3/8)(38-x)² - x(14-3x/16) puis le résultat de votre propre développement et vous verrez que ce sont deux valeurs opposées, je n'ai pas vu vos calculs intermédiaires mais je pense que l'erreur de signe vient du développement de - x(14-3x/16), je suis moi-même tombée dans le panneau du -x(-3x/16), en effet cela fait du - par du - au numérateur et du + par du + au dénominateur, donc au final un quotient positif.. Bref, à présent je fais faire les racines à la main et voir s'il est possible de calculer y avec la valeur exacte de x et non sa valeur approchée (youuuupi quel programme!)
Oui c'est la bonne valeur de y car j'ai une reproduction a l'échelle et en mesurant sur le dessin puis en faisant une règle de 3 j'ai trouvé y=10.9
bien joué, bonne soirée à tous!
Bonjour à tous,
Je viens de voir ce que vous avez écrit précédemment mais je ne comprends toujours pas.
Même si l'on utilise l'équation -9x²/16 + 85x/2 - 1083/2 ou l'équation 9x²/16 - 85x/2 + 1083/2 , delta a toujours la même valeur: 4703/8
Je ne comprends pcomment vous avez trouvé 10,96. Pouvez vous m'en dire un peu plus, s'il vous plait ?
En effet, j'ai constater qu'en remplaçant x par 3 dans (3/8)(38-x)² - x(14-3x/16) et dans mon équation trouvée au départ:
-9x²/16+85x/2-1083/2, on retrouve des valeurs opposées. Mais cela est dû, pour ma part, à ce que j'ai fait au départ: comme il fallait au départ faire un système, j'ai donc dû passer le membre (3/8)(38-x)² de l'autre côté, c'est à dire:
x(14-3x/16)= (3/8)(38-x)²
x(14-3x/16)-((3/8)(38-x)²)
De plus, j'ai ajouté des parenthèses autour (3/8)(38-x)² qui donne ((3/8)(38-x)²), car c'est tout le membre qui passe de l'autre côté non ?
Donc ensuite je trouve, en développant:
14x -3x²/16 - (3/8(x² - 76x + 1444))
14x -3x²/16 - (3x²/8 - 228x/8 + 4332/8)
14x -3x²/16 - 3x²/8 + 57x/2 - 1083/2
-9x²/16 + 85/2 -1083/2
En fait, cela dépend de quelle manière on a créer l'équation: soit en faisant x(14-3x/16)-((3/8)(38-x)²)
ou en faisant (3/8)(38-x)²-(x(14-3x/16))
Voilà. Pouvez m'aider ?
Merci d'avance
Tu as raison j'ai moi aussi remarqué que cela dépendait du sens de la soustraction, enfin peu importe puisque l valeur du discriminant reste la même.
Pour trouver y, il suffit de remplacer x dans l'équation 14-3x/16 par sa valeur exacte (un peu compliquée, certes ^^) trouvée en calculant les racines, tu verras que tu vas trouver 10.96
Ensuite le calcul des aires donne une valeur approchée d'environ 177 m² pour les 3 figures, ce qui prouve l'exactitude des résultats. Il suffit maintenant simplement de faire:
BR=x=16.23
BP=y=10.96
SC=38-x=21.77
AQ=28-y=17.04
ST=3/4(38-x)=12.27
UE=3/4(40-x)-2-y=4.87
Bien sûr ce sont les valeurs approchées car les valeurs exactes sont trop longues à écrire.
Ok merci bien. Je pense que je vais faire comme ça et tampis, je mettrai des valeurs approchées comme réponses. Je ne vois que cette solution.
Merci pour votre aide.
pourquoi quand je fais[ (26-2y+(3/4)(40-x))/2=y ]je trouve[ (224-3x)/16 ]alors que tout en haut on a posté que c'était égal à[ (14-3x)/16 ]pourriez vous me détailler ce calcule merci.


