Inscription / Connexion Nouveau Sujet
Problème ouvert.
Bonjour,
J'ai un DM à faire pour lundi,
je ne comprends pas ce qu'il faut faire.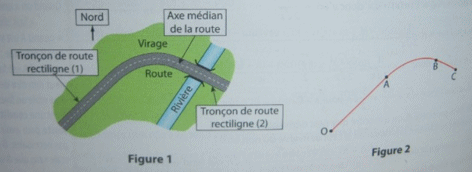
Pouvez-vous m'aider svp ?
Merci d'avance 
* Océane > sarah_93 si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
Salut , juste une idée:
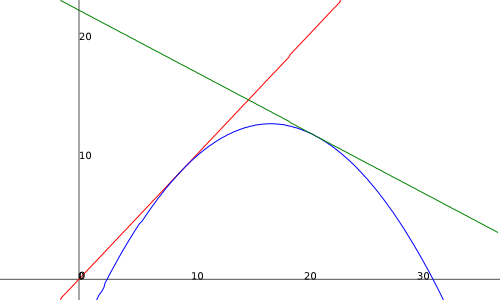
On cherche un arc de parabole de la forme: f(x)= ax2+bx+c
si on suppose qu´il passe par l´origine: f(0)=0 donc c=0
Selon ton ennoncé pour relier A et B il faut 2 conditions: f(9)=9 et f(21)=12
tu substitues et tu aura à résoudre un système de 2 équations avec a et b comme inconnues..
Moi je trouve a= -1/28 et b=37/28
Bonjour, il suffit que tu trouves l'équation d'une parabole passant par A et B et dont les tangentes en A et B soient les droites OA et BC.
(rappel : l'équation d'une tangente c'est y=f'a)(x-a)+f(a))
Je penses que l´idée de Glapion est encore meilleure que la mienne:
J´ai retrouvé une fonction parabolique qui passe par A et B mais cette fonction n´a pas pour tangentes
forcément les droites (OA) et (BC)
donc: grâce aux coordonées des points A,B et C tu peux facilement obtenir les équations des 2 droites
précédentes qui sont de la forme y=Ax+B où A et B sont les constantes à déterminer
Or, f(x)=ax2+bx est la fonction reliant A et B qui doit avoir ces 2 droites comme tangentes à
la courbe en x=9 et x=21
Alors ton problème est de poser f´(9)(x-9)+f(9)=équation de la droite (OA)
f´(21)(x-21)+f(21)=équation de la droite (BC)
(il faudra avant résoudre que tu dérives f(x) ) , ton problème consiste à résoudre ce système
et retrouver les valeurs de a et b.
Un détail ne pas confondre les coéfficients des droites (A et B) avec les points A et B.
Tu pourras appeler ces coéfficients C et D par exemple pour simplifier ta résolution.
Bonsoir,
Calcule l'éq des dtes OA et BC
la tangente en A aura le même coef direct que (OA)
la tangente en B aura le même coef direct que (BC)
en partant du principe que la parabole a pour éq : y=ax²+bx+c et que sa dérivée a pour éq : y=2ax +b
trouve les coef a,b,c
Oui,c´est correct maintenant tu dois résoudre le système avec les équations des tangentes en x=9 et x=21
pour retrouver a,b et c.
Je trouve : a= -1/16
b=17/8
c= -81/16
Sauf erreur.
Pour x=9
x=(18a+b)*(x-9)+81a+9b+c
x=(18a+b)*x -9*(18a+b)+81a+9b+c
x=(18a+b)*x -81a+c
Par identification des termes: (18a+b)=1 ---> b=1-18a
-81a+c=0 ---> c=81a
Pour x=21
-1/2*x+45/2=(42a+b)*(x-21)+441a+21b+c
-1/2*x+45/2=(42a+b)*x -21*(42a+b)+441a+21b+c
-1/2*x+45/2=(42a+b)*x -441a+c
Par identification des termes: (42a+b)= -1/2
-441a+c=45/2
Or, c=81a donc: en substituant a= -1/16 ,évidemment c= -81/16
De plus, b=1-18a soit: b= 17/8
Je n'ai pas compris ça :
Or, c=81a donc: en substituant a= -1/16 ,évidemment c= -81/16
De plus, b=1-18a soit: b= 17/8
Si c=81a on substitue: -441a+(81a)=(45/2)
soit: -360a=(45/2) donc: a= -45/(2*360)= -1/16 après réduire
c=81a=81*(-1/16)= -81/16
Puisque b=1-18a= 1-18*(-1/16)= 1+(18/16)=34/16= 17/8...
Si tu as trouvé a,b et c tu as déjà ta branche de parabole:
y= -1/16x2+(17/8)*x -81/16
la question est répondue.