Inscription / Connexion Nouveau Sujet
Problème pour compléter mon dm de math
Bonjour, j'ai vraiment besoin d'aide j'ai un dm de math à rendre pour *****et depuis plusieurs jours je n'arrive toujours pas à faire la question 2... Je vous met si dessous une image de mon dm.
Début de l'énoncé :
Dans un repère orthonormal (O; i, j) du plan, soit H l'hyperbole d'équation y = 1/x et A le point de coordonnées (-3/2;3/2). A tout réel x non nul, on associe le réel f(x)= AM², où M désigne le point d'abscisse x de l'hyperbole H.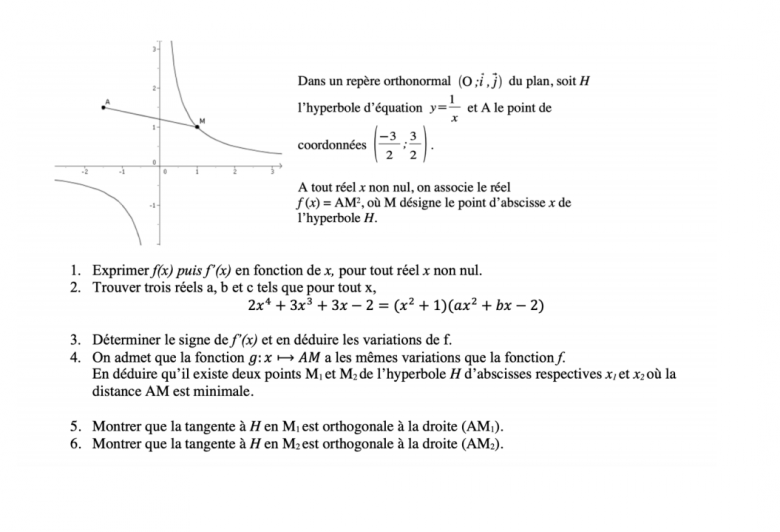
ce que j'ai fait
Pour la première question j'avais trouvé que f(x) = 1/x et que f'(x)= -1/x². Voilà, j'espère que vous réussirez à m'aider parce que je suis vraiment coincé.. J'avais cru qu'il fallait développer dans la question deux mais j'y arrive vraiment pas.
malou edit > ***sujet réorganisé**
Bonjour
je te demande de tout recopier(en réponse à mon message) jusque la question 1 (sinon, on ne pourra pas retrouver ton sujet)
à cette condition, l'image sera autorisée
j'attends...
ensuite on pourra t'aider
Dans un repère orthonormal (O; i, j) du plan, soit H l'hyperbole d'équation y = 1/x et A le point de coordonnées (-3/2;3/2). A tout réel x non nul, on associe le réel f(x)= AM², où M désigne le point d'abscisse x de l'hyperbole H.
Bonjour
Lisez bien le texte : n'est pas la fonction dont la courbe a été dessinée mais elle est définie par le carré de la distance de A à M
rappel
Bonjour,
Pour la question 1, je pense que tu fais une confusion...
On te demande d'exprimer f(x) = AM² !!
Il faut reprendre le cours sur la formule de la distance entre 2 points.
Ah oui merci, effectivement je me suis un peu perdu... Donc pour la question 1 la réponse serait plutôt f(x)= 13/2 et f'(x)=0 ?
Non plus !!
Coordonnées du point A ?
Coordonnées du point M ?
Formule donnée par Hekla (ou encore
si on ne veut pas traîner de racine carrée dans nos calculs...)
Ah je viens de comprendre mon erreur dans la formule de hekla , c'était écrit (xb-xa)² +(yb-ya)² et vous, vous avez mis -
, avec - on trouve donc f(x)=6 et f'(x)= 0 ?
Oups au temps pour moi, j'ai moi-même mal réécrit la formule :
C'est bien (xb-xa)² + (yb-ya)² (et non un signe -) celle de Hekla est bonne.
Par contre ta fonction f est toujours fausse !!
Selon ton énoncé, quelles sont les coordonnées du point A ? du point M ?
Coordonnées de A ok.
Coordonnées de M fausses !!
Ce n'est pas une simple lecture graphique de ton point M...
Ici ton point M est un point variable (et non pas fixé) qui appartient à l'hyperbole.
D'ailleurs, l'énoncé te dit : M désigne le point d'abscisse x de l'hyperbole.
Avec cette info, tu peux déterminer les coordonnées de M : M(... ; ...) ?
Oui, j'avais pas fait attention à ce détail... Mais je suis pas sur de bien comprendre M serait (x;1) ? Vu que M est lié à l'abscisse de H? Ou alors l'ordonnée et l'abscisse bouge donc (x;y) ?
Bonjour Hekla,
Je ne vais pas rester trop longtemps (dans 30 min env.) car c'est la pause déjeuner. 
Mais d'ici là, on aura (peut-être) pas mal avancé...
Oui, ta 2e question est la bonne.
M est un point variable, donc ses coordonnées varient tout autant !!
Donc les coordonnées de M sont (x;y).
Or l'ordonnée y est donnée dans ton énoncé, donc tu obtiens M(x ; ... ) ?
Tout devient clair, désolé j'ai du m'absenter... donc les coordonnées du point M sont (x;1/x). ce qui nous donne : f(x)= (x+3/2)²+(1/x-3/2)²
Bonjour,
Pour la question 2, oui il faut développer le membre de droite et la solution devrait venir...
Tout devient clair, désolé j'ai du m'absenter... donc les coordonnées du point M sont (x;1/x). ce qui nous donne : f(x)= (x+3/2)²+(1/x-3/2)²
Oui c'est bon.
J'ai essayé de simplifier et je suis arrivé à ce résultat qui me parait bizarre : x²+(1/x)²-6x²+9x-6/2x est-ce bon?
Pour la question 2 j'ai essayé de développer le membre de droite... je suis arrivé sur du ax^3+bx²-2x²+ax²+bx-2 et après je ne sais pas quoi faire.
J'ai juste une question comment êtes vous passé de f(x)=x^2+3x+\dfrac{9}{2}-\dfrac{3}{x}+\dfrac{1}{x^2} à f(x)=\dfrac{2x^4+6x^3+9x^2-6x+2}{2x^2} ?
J'ai juste une question comment êtes vous passé de f(x)=x^2+3x+\dfrac{9}{2}-\dfrac{3}{x}+\dfrac{1}{x^2} à f(x)=\dfrac{2x^4+6x^3+9x^2-6x+2}{2x^2} ?
Pour la question 2 j'ai essayé de développer le membre de droite... je suis arrivé sur du ax^3+bx²-2x²+ax²+bx-2 et après je ne sais pas quoi faire.
Il y a des erreurs sur les exposants, attention à : x² * x² = ?
Pour la question 2 j'ai essayé de développer le membre de droite... je suis arrivé sur du ax^3+bx²-2x²+ax²+bx-2 et après je ne sais pas quoi faire.
Il y a des erreurs sur les exposants, attention à : x² * x² = ?
Il faut mettre des parenthèses
on simplifie par
On aurait dû dériver avant de mettre au même dénominateur
Le numérateur est bien le polynôme de la question suivante
Vous avez développé ordonné et réduit le membre de droite, identifiez les deux polynômes
identifier deux polynômes c'est par exemple :
ax² + (b+a)x + c = 4x²-5x +7
on en déduit que : a = 4 b+a = -5 donc b = -9 et c = 7.
Je pense que tu as oublié la question car en relisant la question 2 alors on voit bien qu'il faut identifier avec un polynôme de degré 4, je parle du membre de gauche qu'il faut identifier avec le membre de droite que tu viens de développer.
ainsi que
sont des polynômes de degré 4
en identifiant les coefficients des termes de même degré sont égaux
Donc pour la question deux je dois juste trouver des équivalents, je pense avoir trouver que a= 2 et b= 3 mais pour c est-ce que c'est -2?
Donc pour la question deux je dois juste trouver des équivalents, je pense avoir trouver que a= 2 et b= 3 mais pour c est-ce que c'est -2?
Il n'y a pas de c vous n'aviez que 2 inconnues et
on a l'égalité
Vous pouvez maintenant déterminer le signe de
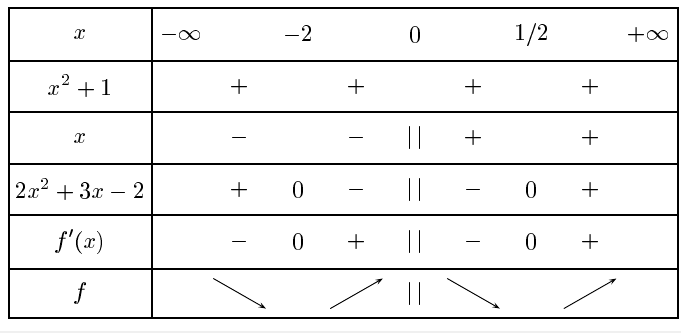
Pour la question numéro 3, je sais qu'il faut faire 2x^4 + 3x^3 + 3x - 2 = 0 mais je n'ai vraiment aucune idée de comment je peux le faire...
À quoi sert la factorisation ? certainement pas à la décoration
Vous savez résoudre des inéquations du second degré.
À quoi sert la factorisation ? certainement pas à la décoration
Vous savez résoudre des inéquations du second degré.
Vous les avez les polynômes
Que voulez-vous d'autre ?
Je vous ai dit que c'était le numérateur de la dérivée que l'on vous demandait de factoriser par la suite
Le numérateur est bien le polynôme de la question suivante
Icelui vient d'être factorisé en
C'est bon j'ai réussi à passer à la question 4 le tableau de signe de la question trois fait + - + .