Inscription / Connexion Nouveau Sujet
Problème trigonométrie
Bonjour a tous
Je vous présente le problème que je rencontre actuellement:
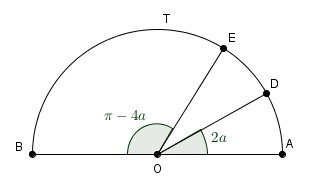
énoncé: Soit un demi-cercle T de diamètre AB. On note O le milieu et R le rayon de T.
Soit "a" un nombre réel compris entre 0 et pi/4
On note "D" et "E" les points de T définis par AOD(cest un angle)=2a et BOE(c'est un angle aussi)=pi-4a
La question est de déterminer DOE mais je ne sais absolument pas quoi faire ... quelqu'un pourrait-il me venir en aide ?
Bonjour,
commencer par faire une figure ...
(en choisissant une valeur quelconque pour a entre 0 et pi/4 radians c'est à dire entre 0 et 45°)
bien entendu la valeur numérique choisie pour tracer cette figure sera immédiatement "oubliée" et appelée "a" partout ... sur les codages que l'on écrit sur cette figure. (2a, pi-4a etc)
ensuite tu as entendu parler d'angles supplémentaires ??
A vrai dire il y a déjà une figure de faite dans l'énoncé ou ADO est un triangle , AHD triangle rectangle et HDO de même.
Oui ce sont les angles qui ont le même sin non ?
tes triangles rectangle ne servent à rien ici et "le même sinus" me semble particulièrement douteux
rien d'autre que ça ne sert dans la figure pour cette question.
Mon prof nous a parler d'angles supplémentaires dans le cadre d'un cercle trigo donc c'est la seule définition d'angle supplémentaire que je connais
Oui j'ai réussi à trouver que DOE=AOD mais je ne vois pas comment le justifier ...


