Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour,
Je rencontre un petit problème dans un exercice de maths concernant les produits scalaires.
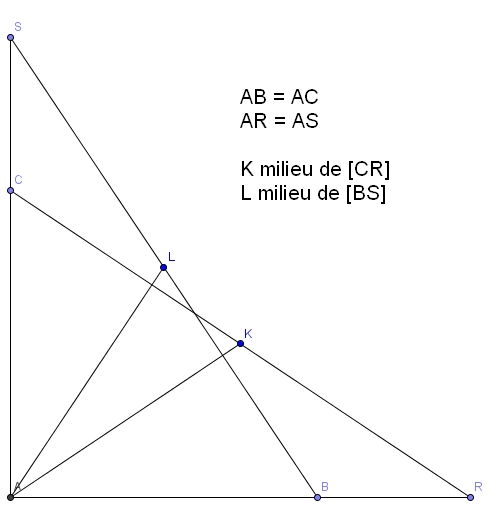
ABC est un triangle rectangle isocèle en A. Pour tou point R de la demi-droite ]AB) on place sur la demi-droite ]AC) le point S tel que AS = AR.
Soit K le milieu de [CR], et L celui de [BS].
1)a. Quelles semblent être les hauteurs des triangles ABS et ACR ?
→ Ma réponse:
(AK) semble être la hauteur de ABS en A.
(AL) semble être la hauteur de ACR en A.
Faut-il que je cite les autres hauteurs des triangles, à savoir (AS) et (AB) pour ABS, et (AC) et (AR) pour ACR ?
b. Démontrer que AAC + AR = 2AK (ce sont tous des vecteurs) et en déduire une décomposition de AK sur les vecteurs AC et AR.
→ Ma réponse:
On fait la relation de Chasles pour 2AK, et on trouve la relation demandée.
pour avoir une décomposition de AK, on reprend la relation trouvée et on divise les deux membres par 2, on trouve ainsi AK = 1/2 AC + 1/2 AR (tous des vecteurs)
c. Décomposer BS sur les vecteur AS et AB.
→ Ma réponse:
On fait de même que la question précédente, et on trouve BS = AS - AB.
d. En déduire AK•BS (vecteurs). Interpréter géométriquement.
→ Ma réponse:
C'est à partir de là que je bloque ... Pour l'interprétation, j'imagine que le produit trouvé sera nul, et donc géométriquement, on en déduit que (AK) et (BS) sont perpendiculaires.
2) Calculer de même AL•CR. (Vecteurs)
→ Ma réponse:
J'imagine qu'il faudrait procéder de la même façon, mais étant bloquée à la question précédente, je n'y ai pas vraiment réfléchi.
3) Résoudre l'exercice par une autre méthode.
→ Ma réponse:
J'y ai vaguement réfléchi, mais pour l'instant, je n'ai pas de piste ..
Merci d'avance pour votre aide 
Bonsoir !
Tout d'abord, merci de me répondre 
Pour la 1)a. est-ce que je dois mettre les 3 hauteurs alors, ou juste une seule ?
Pour la d., c'est justement le développement qui me pose problème. lorsqu'on développe, on trouve 2 produits qui sont nuls, il nous reste donc:
AK.BS = [(AC.AS) + (AR.-AB)]/2
C'est là que je bloque, je sais que:
AC.AS = AC.BS
et AR.-AB = AR.BS
De là, on peut faire une factorisation.
Mon problème, c'est que j'ai des pistes, mais qu'elles n'aboutissent pas ...
Merci d'avance 
1) a. Ouais peut être , si t'as envie de te faire du mal. Je trouve la a) un peu nulle comme question
Après pour le Prod Scal et Bien :
AC et AS sont colinéaires donc tu peux faire sauter les flèches qui devraient se trouver dessus
Pareil pour AR et AB
il est rectangle isocèle donc AC=AB
Et on te dit CLAIREMENT que AS = AR
Tu es convaincu ? 
Ah, d'accord. Tu viens d'éclaircir une partie de cours que j'avais pas encore bien compris, merci 
Donc si je me suis pas trompée dans mes calculs, un moment, on trouve:
AS  (AC - AB)
(AC - AB)
= AS  0
0
= 0
Donc, les droites sont perpendiculaires.
Pour la question 3, est-ce que ce serait possible de résoudre l'exercice en passant par des coordonées, et donc dans un repère ?
Le repère serait (A,B,C), et R(1+x;0) et S(0;1+x). Possible, ou ça ne mènerait à rien ?
bonjour,
j'ai eu le même exercice en ap mais on ne l'a pas corrigé, mardi j'ai une interro dessus. quelqu'un pourrait m'éclairer sur les produits scalaires, les calculs a partir de la question 1) b)?
Bonjour !
j'ai eu cet exercice comme DM note
Et je suis bloque sur la question 1.d
pour AK.BS:
j'ai su que AK.BS=[(AC.AS)+(-AB.AR)]/2
Mais comment continuer ?
Merci d'avance !
bonjour à toi aussi,
un bonjour n'est jamais de trop.
Une proposition :
place toi dans le repère (A, AB, AC), exprime les coordonnées de A, B et C
pose abscisse de R = a
exprime les coordonnées de R(a ; 0), S, K et L
exprime les coordonnées des vecteurs AL et RC et regarde s'ils sont orthogonaux..
à toi !



