Inscription / Connexion Nouveau Sujet
Prouver qu'un triangle est rectangle avec un repère
Bonsoir
Je n'arrive pas à trouver la longueur de deux segments d'un repère avec trois points.
Pourriez vous m'aider s'il vous plait?
Voici l'énoncé:[/u]
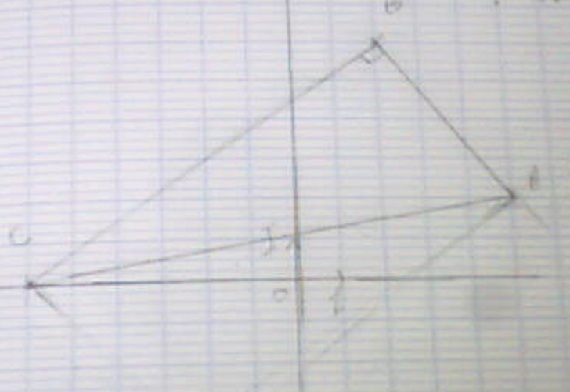
ABC est un triangle dans le repère O, I, J.
Les coordonnées des points sont :
A(5;2)
B(2;6)
C(-6;0)
Prouver que ABC est un triangle rectangle en B.
Donc j'ai fait un repère avec la figure ( joint) et j'ai commencé à trouver la longueur BA puis BC
[u]Voici mon travail:
BA=
(2-5)² + (6-2)²
=(-3)²+(4)²
=-9+16
= 7
BC= (-6+2)²+(0+6)²
= (-4)²+(-6)²
= -16 + (-36)
= -52
Mais là je crois que j'ai tout faux, où-est que je commence à virer?
Qu'est ce qui est faux en premier?
Merci d'avance.
Comment avez vous trouvez 9 ?
Moi j'ai trouvé - 9
Oui je sais qu'après il faut faire
BA²+ BC²= AB²
D'où le triangle est rectangle en B
Mais d'abord, les calculs :pourriez vous précisez?
Est ce qu'on pourrait m'expliquer comment faire, s'il vous plait.
J'ai un devoir demain matin et je suis en train de me préparer.
Je sais bien qu'une longeure ne peut pas être négatif
Mais je ne comprends pas comment faire pour trouver la longueur de BC et BA dans ce repère.
On a que les coordonées, on a pas les longueurs, comment les trouver?
Pour la longueur AB
xA = 5
xB = 2
yB = 6
yA = 2
Pythagore :
AB² = (5 - 2)² + (6 - 2)²
AB² = 9 + 16
AB² = 25
bonjour,
AB²=(xb-xa)²+(yb-ya)²
=(2-5)²+(6-2)²
=(-3)²+(4)²
=9+16
=25
BC²=(xc-xb)²+(yc-yb)²
=(-6-2)²+(0-6)²
=(-8)²+(-6)²
=64+36
=100
AC²=(xc-xa)²+(yc-ya)²
=(-6-5)²+(0-2)²
=(-11)²+(-2)²
=121+'
=125
on constate que AB²+BC²=AC² donc d'après la réciproque de Pythagore le triangle est rectangle
Oui j'ai déjà trouvé
Je continue
BC=100=10
BA=25=5
AC²=BC²+BA²
AC²=5²+10²
AC²=25+100
AC²=125=55
Donc le triangel ABC est bien rectangle en B.
Mon résonnement est correct?
Ah oui gwendolin
J'ai compris, j'avais fait AC aussi
Sans ce calcul on ne peut pas trouver effectivement!
Merci !
tu te compliques la vie avec des racines dont tu n'as pas besoin pour utiliser la réciproque de Pythagpre
tu 'as pas le droit d"écrire que AC²=BC²+AB² quand tu ne sais pas que le triangle est rectangle, il faut comparer AC² et AB²+BC² et conclure
AB²=(xb-xa)²+(yb-ya)²
=(2-5)²+(6-2)²
=(-3)²+(4)²
=9+16
=25
BC²=(xc-xb)²+(yc-yb)²
=(-6-2)²+(0-6)²
=(-8)²+(-6)²
=64+36
=100
AC²=(xc-xa)²+(yc-ya)²
=(-6-5)²+(0-2)²
=(-11)²+(-2)²
=121+'
=125
On a pas le droit, on doit mettre
C'est dans mon cour.
Distance de deux points dans un repère orthonormé
Propriété
Dans un repère orthonormé, on considère les points A (xA;yA) et B(xB:yB).
La distance entre A et B est : AB =
(xB-xA)²+(yB-yA)²
Annuler
connectez vous