Bonjour, j'ai du mal avec une question ce cet exercice car je ne pense pas l'avoir vu en cour mais c'est un devoir donc j'aimerais bien un peu d'aide, je vais répondre à toutes les questions si il y a une erreurs peut-on m'aider?
voici l'exercice:

Dans cet exercice toutes les dimensions sont données en cm.
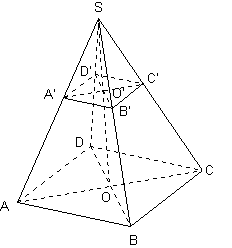
La pyramide SABCD est telle que:
* la base ABCD est un carré de centre O tel que AC=12
* les faces latérales sont des triangles isocèles en S
* les hauteurs [SO] mesure 8
(La figure n'est pas aux dimensions réelles).

1) Dans le triangle SOA rectangle en O, montrer que SA = 10.
2) Sachant que AB = 62, montrer que l'aire du carré ABCD est 72cm²
3) Montrer que le volume de la pyramide SABCD est égal à 192 cm3.
4) Soient A' un point de [SA] et B' un poind de [SB] tels que SA'= SB'= 3.
   Montrer que (AB) et (A'B') sont parallèles.
5) La pyramide SA'B'C'D' est une réduction de la puramide SABCD, calculer le coefficient de réduction.
6) Calculer le volume de la pyramide SA'B'C'D'.

REPONSES:
1- On a SO=8cm et AO = AC/2 = 12/2 = 6 et le triangle SOA est rectangle en O donc d'après le théorème de pythagore on a:
    SA² = SO² + AO²
        = 8² + 6²
        = 100
donc SA = 100
        = 10                       On a bien SA égal à 10cm.

2- Formule pou l'aire d'un carré:
      A = cxc
      A = 62 x 62
        = 6 x 6 x 2 x 2
        = 36 x 2
        = 72                       On a bien l'aire du carré qui est égal à 72cm².

3- Formule pour le volume d'une pyramide:
      V = 1/3 x B x H
      V = 1/3 x 72 x 8
        = 192                       On a bien le volume du carré égal à 192cm3

4- * SA = SA'+ A'A = 3 + 7 = 10. et SB = SB' + B'B = 3 + 7 = 10
   * On a les droites AA' et BB' qui sont sécantes en S.
   * On a d'une part: SA'/SA = 3/10
    et d'autres part: SB'/SB = 3/SB
SB dxg égale à 10 cm comme tout les autres côtés car SOA est un triangle rectangle en O et dans une pyramide, si la hauteur de celle-ci est parallèle à la base alors les côtés sont de même longueur: SA = SD = SC = SB = 10cm,
donc SB'/SB = 3/10
et on a bien : SA'/SA = SB'/SB
Donc d'après la réciproque du théorème de Thalès, les droites (A'B') et (AB) sont parallèles.

5- je ne sais pas.
6- je connais la formule pour le volume d'une pyramide mais il me faudrait l'air et la base de celle-ci, mais d'abord le coefficient pour tout calculer.

merci d'avance.