Inscription / Connexion Nouveau Sujet
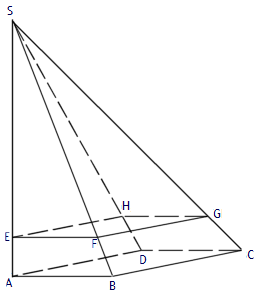
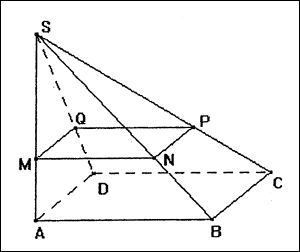
pyramide a base rectangulaire
Bonjour pourriez vous m'aider avec cette exercice type brevet svp .
1. Calculer le volume de la pyramide SABCD.
2. Démontrer que SB = 17 cm.
3. On note E le point de [SA] tel que SE = 12 cm et F le point de [SB] tel que SF = 13,6 cm.
Montrer que (EF) et (AB) sont parallèles.
4. On coupe cette pyramide par le plan passant par E et parallèle à la base de la pyramide.
La pyramide SEFGH, ainsi obtenue, est une réduction de la pyramide SABCD.
a) Quel est le coefficient de cette réduction ?
b) En déduire le volume de la pyramide SEFGH en fonction de .
Avec explication si possible
Merci d'avance 
Bonjour
1. Calculer le volume de la pyramide SABCD.
V=aire de ABCD*SA/3
Il faudrait avoir les dimensions
Je n'avais pas vu ta réponse avant de poster, mais je ne vois pas ce qui t'empêches de calculer le volume, un peu de courage, on ne va pas faire les calculs à ta place
Comment je trouve l'aire de la base ?
la base est un rectangle......tu sais calculer l'aire d'un rectangle, je suppose

non, une aire ne s'exprime pas en cm mais en cm²..
l'aire du rectangle de base est donc égale à 88 cm²
Mais aprés j'ai du mal
peux-tu préciser où exactement ?
Donc le volume de la pyramide sabcd et de 88cm carré .
J'ai du mal avec la question 3 je me rappel plus comment on fait
tu dois utiliser la réciproque du théorème de Thalès...
pour cela calcule SE/SA puis SF/SB et démontre que ces deux quotients sont égaux
pour la question 2 il faut appliquer le tehorème de thales ?
non, c'est Pythagore dans le triangle SAB
pour la question 3 il faux que j'applique la reciproque de thales mai je connai pas la longueur SA comment je fais ?
relis ton post du 29 avril à 18h 26 ...
SA = 15 cm
tu as bien sorti cette mesure de quelque part....