Inscription / Connexion Nouveau Sujet
Python et probabilités
À fin de simplifier les choses, on considère aura qu'une année compte systématiquement 365 jours.
1) on s'intéresse à une classe de 26 élèves.
a) Combien y a-t-il d'issue possible pour les dates d'anniversaire de tous les élèves de cette classe ?
b) déterminer la probabilité qu'il y est au moins deux élèves de cette classe qui est la même date d'anniversaire. On pourra commencer par calculer la probabilité de l'événement contraire. Vous donnerai la réponse sous forme d'un pourcentage arrondi au dixième.
2) Soit k un entier supérieur ou égal à deux. On note pk la probabilité que, dans un groupe composé de k personnes, au moins deux aient la même date d'anniversaire.
a) justifier que pk = 1-[(Ak365)/365k)] ou Ak365 = n!/(n-k)!
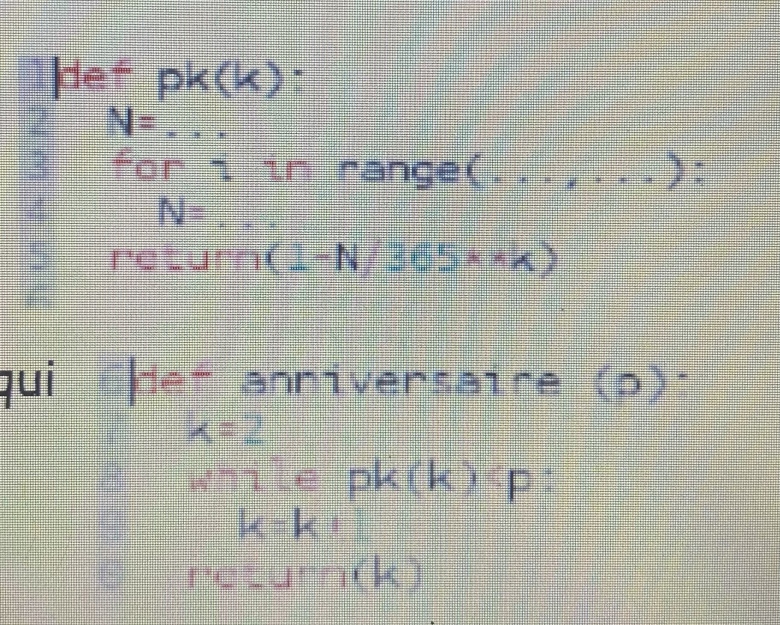
b) recopier et compléter le script ci-contre en python afin qu'il retourne la probabilité pk pour une valeur de k donnée.
Programme python en lien ci dessous.
3) On donne si contre le script de la fonction anniversaire qui fait appel à la fonction pk précédente.
a) que retournant l'appel anniversaire (0.005) ?
b)Qu'elle est le rôle d'une telle fonction ?
c) programmer les deux fonctions puis interpréter le résultat retourné par l'appel anniversaire (0,9).
Pouvez vous je ne comprends rien au premières questions et à phyton.
Non
Pour le deuxième éleve, il y encore 365 cas possibles.
Donc pour les 2 élèves, il y a 365*365 cas possibles ou 3652
Pour le troisième élève il y a encore 365 cas possibles
Soit pour près 3 elèves :............. Cas possibles.
Oui c'est la calculatrice 😂
Pour la deux la probabilité de l'événement contraire c'est la probabilité qu'il y est au moins deux élèves qui n'aient pas le même date d'anniversaire.
Par contre pour calculer la probabilité je ne sais pas comment faire.
Pour le 1er élève, il y a 365 choix de jours.
Deuxième elève : il en reste 364
Troisième élève: 363
Pour le dernier élève, il en restera ....
Nombre de choix possibles
365*364*363*..................*........=.....
Ce résultat sera le nombre d'éléments de l'événement contraire.
Rne donne pas des résultats de cette manière
Complète
( on a 26 élèves)
365*364*363*362*361*..................*........=.....
365*364*363*362*361*.......*339 5,67*1068
5,67*1068
Mais je ne vois pas comment calculer la probabilité de l'événement contraire.
Oui
Une proba ne dépasse pas 1
A revoir
Je vais devoir stopper
Je n'ai pratiquement plus de batterie
Pour répondre à la question
b) déterminer la probabilité qu'il y est au moins deux élèves de cette classe qui est la même date d'anniversaire.
Il te suffira de calculer 1-p(évènement contraire)
Je regarderai une fois la batterie rechargée
D'accord bonne soirée
J'ai trouvé que proba de l'événement contraire = 0,40176 soit 40,2 %
Donc proba que au moins deux élèves est là même date d'anniversaire = 1-0,40176 = 0,59824 soit 59,8 %.
Bonjour,
Par curiosité ,j'ai voulu voir la probabilité que deux élèves aient une
date d'anniversaire commune.
Je trouve 60.3 %
salut
pour la généralisation à la 2/ tu fais la même chose pour une classe de k élèves que ce que tu as fait pour la classe de 26 élèves ...
Je ne comprends pas ce que vous venez de dire. Pour la classe de 26 élèves j'ai fait la probabilité de l'événement contraire. Ici, je me perd entre K, N ect...
salut
cas possibles : 365*365*365*.....365 (k fois) comme te l'a suggéré Kenavo que je salue
P( au moins 2 eleves on la meme date anniversaire ) = 1-P( tous les élèves ont des dates d'anniversaires différentes)= .....
touts les eleves ont des dates d'anniversaire différentes alors cas favorables :
365*364*363*.........*( a toi de me donner le dernier terme sachant qu'on a à faire à k eleves)
J'ai trouvé que pk= 1-[(365!)/(365-k)!*365k].
Mais je sais pas quoi faire pour justifier maintenant.
Bonjour,
J'ai un exercice de maths mais je ne comprends pas quoi faire.
À fin de simplifier les choses, on considère qu'une année comporte 365 jours.
Soit k un entier supérieur ou égal a 2. On note pk la probabilité que dans un groupe composé de k personnes, au moins 2 est la même date d'anniversaire.
1) Justifier que pk = 1- (Ak365)/365k ou Ak365 = n!/(n-k)!
2) Compléter le script si contre afin qu'il retourne la probabilité pk pour une valeur de k donnée.
Programme :
Def pk(k):
N= .......
For i in range (.....,.....):
N= ......
Return(1-N/365**k)
Ce que j'ai fait :
A la question 1, j'ai trouvé 1-[(365!)/[(365-k)!*365k]] mais je ne sais pas quoi faire après. Et même je ne sais pas si c'est bien.
*** message déplacé ***
Bonsoir
 extrait de
extrait de Q24 - Moi, tout ce qui m'intéresse, c'est d'obtenir de l'aide. Vos règles du forum, je n'en ai rien à faire !
sans commentaires


 ) :
) :
 :
:
 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site
