Bonjour,
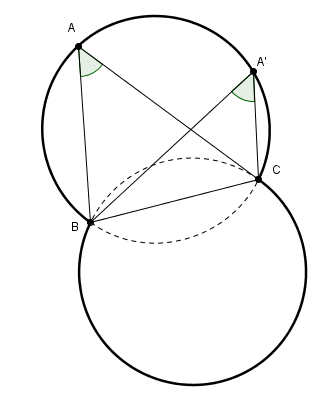
A est n'importe où sur "l'arc capable" de l'angle donné, lieu des points d'où on "voit" BC sous l'angle donné.

(théorème des angles inscrits)

Bonjour,

Comme l'indique mathafou, ton problème est indéterminé.
Ton titre "triangulation" et les points d'appuis donnés en coordonnées, laissent à penser que ton exercice à pour cadre la topographie et les calculs topométriques. Est-ce le cas?

De toute manière, pour déterminer les coordonnées de ton point , tu as besoin d'une donnée supplémentaire par exemple:

  - Soit un point ainsi qu'un angle (BAD ou CAD) connus. On parle alors de "relèvement"

  - Soit une distance (AB ou AC) connue.  

Dans tous les cas il existe des formules qui donnent les coordonnées de ton point en fonction des données (par exemple pour le relèvement les coordonnées de trois points et deux angles).

oui ce serait pour un relevé topographique avec les angles entre (AB) et le nord et (AC) et le nord. et les coordonnés de x y de A et B qui seraient des points de repères.

si tu connais A et B l'angle entre (AB) et le nord n'est pas une donnée supplémentaire !!!

la seule inconnue là dedans étant C, et il est tout aussi indéterminé que dans l'autre cas, est c'est encore plus évident : il est n'importe où sur la droite qui fait l'angle (AC) avec le nord et passe par A.

A la réflexion, ce serait alors un calcul d'intersection et pas de relèvement.

  Et il existe aussi des formules pour ce calcul qui donnent directement les coordonnées de   connaissant celles de et et tes deux angles

Bonjour,

Comme le montre le beau dessin de mathafou, il y a une infinité de solutions qui appartiennent aux deux cercles, donc ceci ne te permettra pas de localiser ton point A.

Normalement il te faut un troisième point D au minimum, ainsi ceci te generera d'autres cercles dont l'intersection avec les deux cercles précédents te donnera ton point A.

Pour la résolution, on utilisera la Loi des cosinus de Al-Kashi, ainsi que le fait que l'angle au centre B0C est le double de l'angle BAC.

l'énoncé est à géométrie variable ...

C'est le moins qu'on puisse dire! Je m' en étais rendu compte!

Sans jouer au devin devant sa boule de cristal, je pense que cette dernière version est la bonne. D'où un simple calcul d'intersection selon le vocabulaire consacré en topographie.