Inscription / Connexion Nouveau Sujet
Racine carré de vecteur
Bonjour/Bonsoir,
Je fais une activité préparatoire sur le chapitre du produit scalaire de 1ère et je suis tombé sur une question dans un exercice, où il m'est demandé d'effectuer une somme de vecteurs dont l'un est à la racine carrée. Pourriez-vous s'il vous plaît m'aider et me donner la formule de calcul des coordonnées d'un vecteur à la racine carrée ?
Merci pour votre aide 
Racine carrée de Vecteur ???? C'est la première fois que tu vois ça ? Et probablement la dernière aussi.
Ca n'existe pas.
Racine carrée de Vecteur ???? C'est la première fois que tu vois ça ? Et probablement la dernière aussi.
Ca n'existe pas.
Bonsoir, voici la question (cf. image en pièce-jointe)
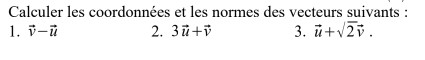
Quand tu vois , tu le comprends comment ?
C'est le vecteur multiplié par le nombre
.
Pareil, , c'est le vecteur
multiplié par le nombre
Il ne faut pas confondre (qui ne veut rien dire) et
ou pour que ce soit plus lisible :
Il ne faut pas confondre (qui ne veut rien dire) et
Quand tu vois
C'est le vecteur
Pareil,
Il ne faut pas confondre
ou pour que ce soit plus lisible :
Il ne faut pas confondre
Ah d'accord merci beaucoup pour ces éclaircissements, je comprends mieux maintenant



