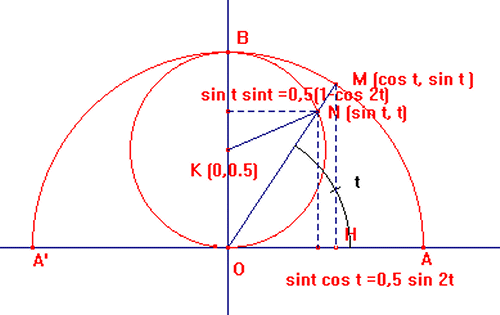
Un point M décrit le demi-cercle de diamètre [AA']. Soit H la projection orthogonale de M sur (AA'). On construit le point N du segement [OM] tel que ON = MH.


Le but du problème est de déterminer de deux facons le lieu décrit par le point N.
On supposera que OA = 1

1 - On considère le repère orthonormal direct (O;i;j) avec (vecteurs) OA = i et OB = J et on pose : ( i; OM ) = téta

a) Déterminer les coordonnées cartésiennes de M dans (O;i;j), des coordonnées polaires de N dans (O;i) et préciser l'intervalle que décrit téta quand M décrit le cercle.

b) Démontrer que : (vecteur) ON = 1/2 [sin2tétai + (1-cos2téta)j]

c) On désigne par K le milieu de [OB]. Exprimer (vecteur) KN en fonction de i et j et en déduire que : KN =0.5
Que peut on en déduire pour le point N ?

d) Démontrer que les coordonées polaires de N dans le repère (K;-j) sont (0.5;2téta).

e) Conclure sur le lieu des points N lorsque M décrit le demi-cercle AA'


Mes réponses:
a) x = r cos téta
   y = r sin téta

donc comme OA = 1 et que M appartient au cercle, alors x = cos téta et y = sin téta

Or pour les coordonées polaires, là je bloque, je ne vois pas comment à partir des données on peut trouver les coordonnées de N ...
Aidez-moi, merci d'avance...