Inscription / Connexion Nouveau Sujet
Réduction et pyramide
Bonjour à tous,
J'ai pratiquement terminé cet exercice de mon DM, mais je n'arrive pas à répondre à la dernière question :
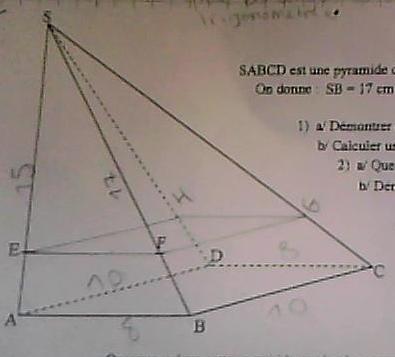
SABCD est une pyramide de base rectangulaire et de hauteur [SA].
On donne : SB=17cm AB=8cm BC=10cm
1)a- Démontrer que SA=15cm
b- Calculer une valeur approchée de l'angle SBA
2)a- Que dire du triangle SAD (justifier la réponse)
b- Démontrer alors que SD= 5 13
13
3)Calculer le volume V1 de la pyramide SABCD.
On a placé E sur [SA] tel que SE=12cm et F sur [SB] tel que SF=13,6cm
4)Démontrer que les droites (EF) et (AB) sont parallèles.
On coupe alors cette pyramide par le plan passant par E et parallèle à sa base.
5)a- Dessiner la section obtenue (G sur [SC] et H sur [SD])
b- Quelle est la nature du quadrilatère EFGH ? (Justifier)
6)a- Calculer le coefficient qui permet de passer des dimensions de SABCD à celles de SEFGH.
b- En déduire SH (valeur exacte)
7)Calculer le volume de SEFGH.
8) Expliquer où il aurait fallu placer E pour que la petite pyramide ait un volume 8 fois plus petit que celui de SABCD.
J'ai trouvé pour le volume de SABCD, 400cm3
Volume de SEFGH, 204,8cm3
Coefficient 4/5, soit 0,8.
Voilà, si vous pouviez m'aide pour la dernière question!
Et merci d'avance pour votre aide!
Bonjour,
8)
Quand le coeff de réduction des mesures d'un solide est k , le coeff de réduction de son volume est k3. A SAVOIR !
8 fois plus petit donne : k=1/8
Si k3=1/8 alors k=1/2
car (1/2)3=1/8
Donc il faut placer E au milieu de [SA].
Je ne sais pas comment tu as fait pour calculer le volume de SEFGH mais tu pouvais faire ainsi:
V (SEFGH)=V (SABCD)*0.83=400*0.83=204.8 cm3
Je ne comprends pas...
Je sais que les volumes sont multipliés pas k3, mais je ne comprends les calculs que tu as fait pour dire qu'il fallait placer E au milieu de [SA].
Pour le volume, je l'ai calculé comme tu as fait.
Pour moi , ce serait une résolution d'équation
Comme ton volume est de 400, pour avoir qch de 8 fois plus petit cela donne un volume de 50 cm3.
Volume de pyramide = 1 tiers fois aire base fois hauteur
50 = (EF*FG*SE)/3
tu poses SE = x
et tu exprimes EF et FG en fonction de x.
Je pense que c'est un truc comme ca.
Chloeeee, tu comprends que si le coeff de réduction est 0.8 , on multiplie le volume de la grande pyramide par 0.83 pour obtenir le volume de la petite.
J'explique donc autrement ma technique. On veut diviser le volume de la grande pyramide par 8 pour obtenir le volume de la petite.
OK ?
Mais diviser par 8 , c'est multiplier par 0.125 car 1/8=0.125.
Donc on fait : 400*0.125=50 ( 50 comme le dit Ange85)
Mais 0.125=0.53
Donc j'aurais pu faire : 400*0.53.
Ce qui prouve que le coeff de réduc est 0.5.
Mais 0.5=1/2
Donc le coeff de réduc est 1/2.
Mais c'est plus simple de voir que 8=23
donc que si k3=1/8 alors k=1/2
car (1/2)3=1/8
Je ne comprends pas non plus, puisque le volume de la petite pyramide est de 204,8cm3, et non de 50cm3.
Mon 50 est pour ta dernière question. On te demande ou placer E si on veut une pyramide 8 fois plus petite. Donc ca n'a aucun rapport avec ton calcul précédent de volume. 400 / 8 = 50 Donc on te demande ou mettre E pour avoir une pyramide de volume 50 cm3


