Inscription / Connexion Nouveau Sujet
Relation / Fonction
Bonjours,
Je suis en 1er Sti2D, J'aimerais si possible que chaque réponse sois expliquer car j'aimerais comprendre et non avoir les réponses brut et que je comprenne rien par la suite. ^^'
Voici mon exercice :
On considère la fonction f définie sur l'intervalle par :
1. a) Déterminer la fonction dérivée de la fonction f.
b) En utilisant la relation , montrer que, pour tout nombre réel x de
:
2. Résoudre dans l'intervalle l'équation produit :
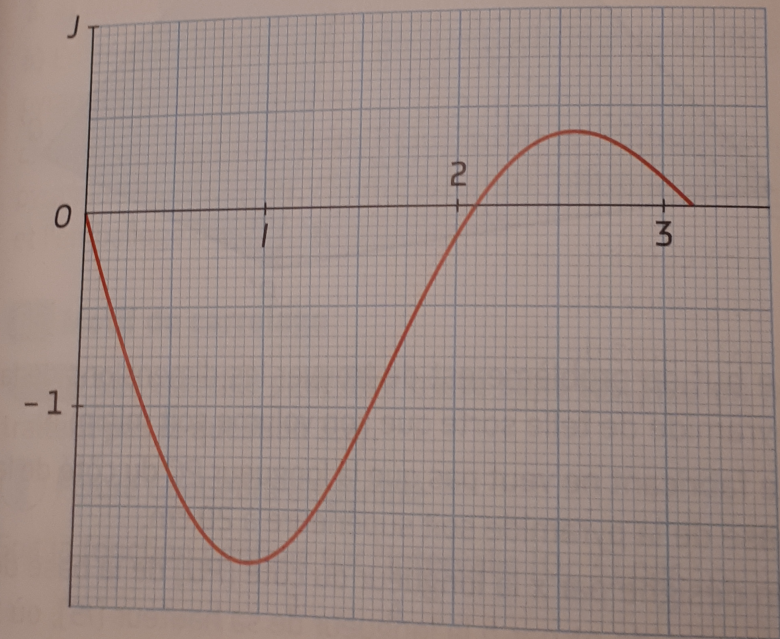
3. En s'appuyant sur la représentation graphique de la fonction dérivée f' donnée ci-dessous, dresser le tableau de signes de f'(x) pour tout réel x de . (Voir Image)
4. Déduire de la question 3. le tableau de variation de la fonction f sur l'intervalle . Préciser les ordonnées des points dont l'abscisse x vérifie f'(x) = 0.
5. Dans un repère orthonormal (O,I,J) d'unité graphique 1 cm, tracer la courbe représentative de f sur l'intervalle . (Je le ferais moi même grâce aux autres réponse)
Pour la 1. a) j'ai trouvé la dérivé suivante :
bonjour
ta dérivée est juste
utilise l'indication qu'on te donne dans l'énoncé maintenant pour factoriser cette dérivée
Je ne comprend pas comment on peux faire une équation avec cosinus et sinus en même temps , j'ai chercher sur internet mais aucune solution véritable.
Donc si vous avez une quelconque explications, je suis preneur ! :p
Bonjour,
Je prends le relai de malou une minute pour te décoincer.
Ton équation est un produit égal à zéro.
Pour qu'un produit soit nul, il faut et il suffit qu'un des facteurs du produit soit nul.



