Annuler
connectez vous
- Cours sur les triangles : construction et droites remarquables - cinquième
- Exercices sur les nombres en écriture fractionnaire - cinquième
- Dix problèmes pour revoir les acquis de la sixième - cinquième
- Quatorze Exercices pour démarrer le calcul numérique - cinquième
- Seize Exercices portant sur le programme de cinquième
- Vocabulaire cinquieme
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. CinquièmeForum de cinquième TrianglesTopics traitant de triangles [tout]Lister tous les topics de mathématiques
Niveau cinquième
Rendez-vous.
Posté par Leeaa
Bonjour ! 
J'ai un exercice de géométrie , que je n'arrive pas tellement à faire.
Qui pourrais m'aider ?
Voici l'énoncer.
Rendez- vous est pris auprès des trois mousquetaires pour un duel : il serait juste que le duel ait lieu à égale distance de leurs maisons.
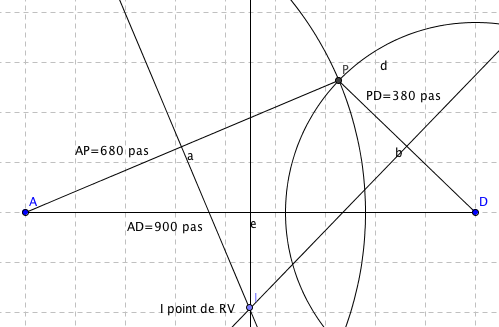
Aramis (A) habite à 680 pas de Porthos (P), qui habite à 380 pas de d'Artagnan (D) ; 900 pas séparent Aramis et d'Artagnan.
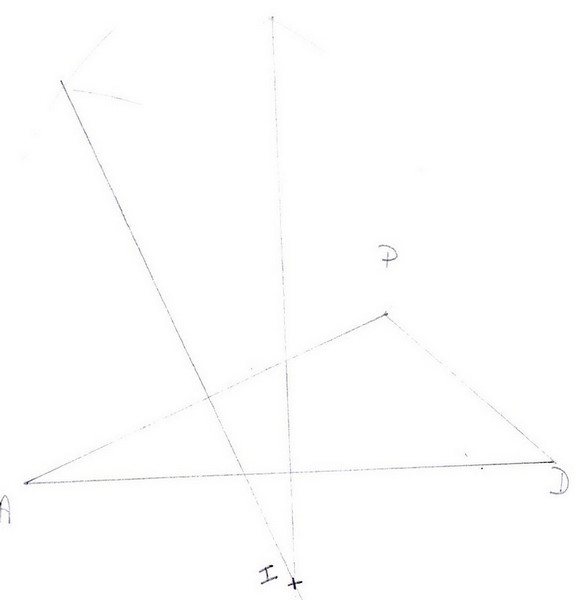
a) En représentant 10 pas par 1mm , construire un triangle qui figurera les trois maisons.
Je pense l'avoir réussie pour les mesure j'ai mis , 68mm pour [AB] , 38mm pour [PD] et 90mm pour [DA] .
b) Construire le point I , idéale pour le duel. ( Justifier la construction sur votre copie).
J'ai construis le point I , en tracent deux médiatrices du triangle.
Pour la justification , j'ai nommé la propriété ;
Si un point appartient à la médiatrice d'un segment alors il est équidistant des extrémités de ce segment. ( Pour la justification je ne suis pas sur . )
c) Justifier l'affirmation d'Athos , qui prétend que si AD avait mesuré 1060 pas , il n'aurait pas été possible de fixer un point de rendez-vous équidistant des trois habitations.
C'est là , que je n'ai pas réussie. Qui peut m'expliquer ?
bonjour
essaie de construire le "triangle" de dimensions 680;380;1060 !!!
(souviens toi de l inegalité triangulaire)
Il n'aurais pas était possible de construire le triangle.
Dans un triangle la longueur du plus grand coté doit être inférieur ou égale à la somme des deux autres cotés.
bonjour,
tous points équidistant d'un point du plan appartient à un cercle de centre ce point
Porthos est à 680 pas d'Aramis
--> trace un cercle de 68 mm de centre A (maison Aramis) et choisis un point P lieu de la maison de Porthos
la maison de d'Artagnan est à 380 pas de celle de Porthos
--> trace un cercle de rayon 38 mm de centre P
la maison de d'Artagnan est à 900 pas de celle de d'Artagnan
-->trace un cercle de centre A et de rayon 90 mm, il coupe le cercle précédent en D = maison de d'Artagnan
pour être à égale distance de A, P et D, il faut que le point I soit sur les médiatrices de [AP] et [DP]
tous pont équidistant des extrémités d'un segment appartient à la médiatrice de ce segment
c)condition d'existence d'un triangle :
AD<=AP+PD
AD=1060
AP+PD=680+380=1060
on a un triangle plat