Inscription / Connexion Nouveau Sujet
repere orthonormal / fonction f...
bonjour,
je m'appelle Mylene, je suis au cned et j'ai beaucoup de mal a faire un exercice dans un de mes devoir. Je vous donne l'ennonce et les questions:
La courbe (C) ci-contre dans le repère orthonormal (0;(i)⃗,j⃗), est la courbe représentative de la fonction f définie sur par f(t) = t^2 - 1.
*alors, je vous explique: je ne peux pas vous envoyer le schema alors j'en est trouver un sur internet: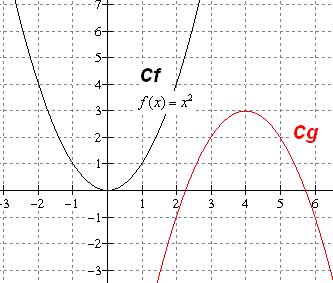
c'est la courbe de gauche, sauf que dans mon exercice, au lieu de passer sur le 0 elle dessand jusqu'a [0;-1].
et les questions sont:
1) a) Déterminer les images par f des nombres 3 et √2.
b) Déterminer les valeurs exactes des solutions de l’équation
f (t) = 5.
2) Indiquer de deux façons différentes le signe de f t ( ) selon
les valeurs de t :
a) graphiquement
b) par le calcul.
3) Quelle est la fonction affine g représentée par la droite d ?
4) Résoudre l’inéquation f (t) ≤ g (t):
a) graphiquement
b) par le calcul.
voila, c'est tout. J'espere que j'ai ete claire 
et pardonnez moi si il y a des fotes d'orthographes 
Un grand merci d'avance, J'ai vraiment besoin de votre aide 
Bonjour,
pour la fonction f(t)=t²-1, on n'a pas forcément besoin du graphe, mais pour t'aider jusqu'à la fin de ton exo, on a besoin de quelques infos complémentaires sur la droite affine d dont tu ne dis rien
je te transmets ce message avant de répondre au reste
quand tu as une fonction f(t) l'image d'une valeur a par cette fonction est la valeur f(a)
donc pour avoir l'image de 3 et de 
2,
dans f(t)=t²-1, on remplace t par 3 puis par 2
f(3)=8
f(2)=1
écrire
f(t)=5, c'est écrire
t²-1=5
t²=6
et les racines de cette équation sont +6 et -6
si tu as tracé correctement le graphe, tu vois que la courbe qui part de +
décroit et passe sous l'axe Ox entre les valeurs -1 et +1 de t,
c'est donc entre ces 2 valeurs de t que la fonction sera négative.
par le calcul tu écris
f(t)=t²-1<0
(t-1)(t+1)>0
et il te faut alors faire le tableau des signes tel que tu l'as appris en seconde
et tu vois que f(t) est négatif pour les valeurs de t comprises entre -1 et +1
Annuler
connectez vous