Inscription / Connexion Nouveau Sujet
resolution d'inequation.........
bien le salut a vous me revoila avec un nouvel exemple cette fois traitant des inequations.......
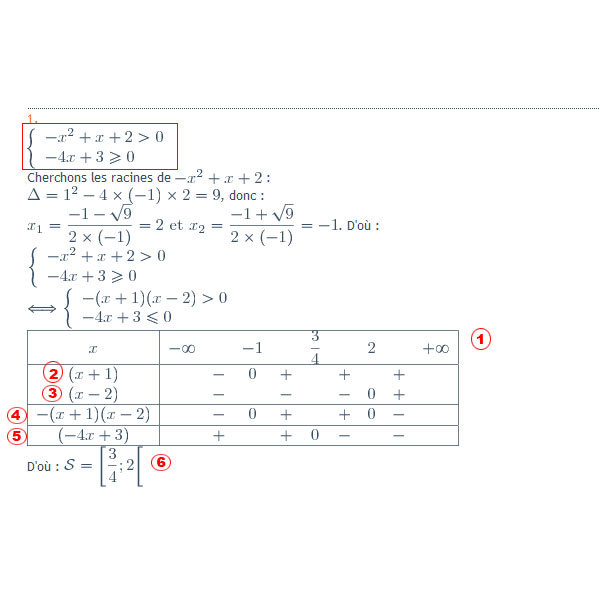
bon l'exemple est sur l'image jointe avec la solution.
donc on a un syteme d'inequation a resoudre.
et comme la premiere inequation est un trinome du second degré on doit trouver les racines de ce dernier pour cela on doit calculer:
 qui vaut b2 - 4 a*c
qui vaut b2 - 4 a*c
 = (1)2 - 4 (-1 * 2)= 1 + 8 = 9
= (1)2 - 4 (-1 * 2)= 1 + 8 = 9
 = 9 (
= 9 ( > 0) donc :
> 0) donc :
x1 = -b - 
 / 2 * a
/ 2 * a
x1 = - 1 - 3 / 2 * (-1) = 2
x2 = -b + 
 / 2 * a
/ 2 * a
x2 = - 1 + 3 / 2 * (-1) = - 1 d'ou
1) - ( x + 1 ) * ( x - 2 ) pour cette forme j'aimerais bien qu'on m'explique pourquoi on a mis ( x + 1 ) et pas ( x - 1) pareil pour ( x - 2 ) car dans notre solution,celle des racines on a trouver x1 = 2 et x2 = -1 .
maintenant revenant au tableau des signes :
la premiere ligne designe les valeur de x dans nos deux inequations pour lequelles ces dernieres (inequations) sont  0 en partant de -
0 en partant de - vers +
vers + c ca ?
c ca ?
pour la deuxieme ligne on a la forme factoriser de notre premiere inequation (trinome) a gauche et les signes et les valeurs (0) a droite quelqu'un peut il m'expliquer svp comment je dois mis prendre pour trouver les signer enfin s'il y a une regle generale ainsi que pour le reste du tableau .............
et pour finir pourquoi on a pas admis - 1 comme solution [sur l'image](6).
Bonjour Adel .
Si les racines de l'équation du second degré sont
x = -1 et x = 2
cela signifie que f(-1) = 0 , et f(2) = 0
et que l'on peut donc mettre f(x) sous la forme
f(x) = - (x+1)*(x-2)
puisque f(x) doit s'annuler pour x = -1 et x = 2 ...
La 1ère ligne du tableau recense toutes les valeurs de x qui nous intéressent ici, concernant la résolution du système . Comme on cherche le signe des fonctions, on indique toutes les valeurs qui annulent l'une ou l'autre des fonctions, puisque c'est à partir de ces 0 que l'on détermine le signe de chaque facteur .
Comme on s'est attaché précédemment à écrire chaque fonction sous la forme d'un produit de binômes,
en dessous, on place chaque binôme sur une ligne séparée , et on indique son signe dans chaque intervalle par rapport à 0 .
Une rêgle du cours (tu chercheras) indique que (x+1) est négatif pour les valeurs x <-1 (c'est du reste facile à vérifier), donc positif pour les valeurs supérieures ...
Le signe final est donné par le produit des signes , intervalle par intervalle .
le signe final tu veux dire la ligne (5) du tableau? j'aimerais bien que donne plus d'explication sur ce point stp 
Non, ici, il n'y a pas de ligne 5 bis, pour donner la synthèse finale .
Elle a été remplacée par le résultat (6) .
Exemple : pour x < -1
le trinôme (ligne 4) est négatif (signe - dans la ligne 4 entre x = -oo, et x = -1)
la 2ème expression (ligne 5) est positive : signe + pour le même intervalle.
Donc le signe de la ligne 4 ne correspond pas à ce qui est demandé .
Par contre, pour l'intervalle suivant, les deux signes (lignes 4 et 5) sont les signes qui correspondent aux 2 résultats demandés . Ce résultat est indiqué à la ligne 6.
derniere question si tu permet les solution comment doit on faire pour les choisir par exemple dans notre tableau il ya trois chiffre ( - 1 , 3/4 , 2) pourquoi on a choisi seulement (3/4 , 2) et pas -1 ?
amicalement adel.
L'exercice te demande " l'intervalle " dans lequel les 2 inéquations sont vérifiées ...
La 1ère inéquation demandait à être positive : d'après la tableau, elle est positive dans cet intervalle.
La 2ème inéquation devait être positive ou nulle: dans le même intervalle, on avait ce résultat .
C'est donc bien cet intervalle qui convient pour répondre A LA FOIS aux 2 inéquations .
Je pense que tu devrais revoir (ou voir ? ) sérieusement ton cours sur ce chapitre !


