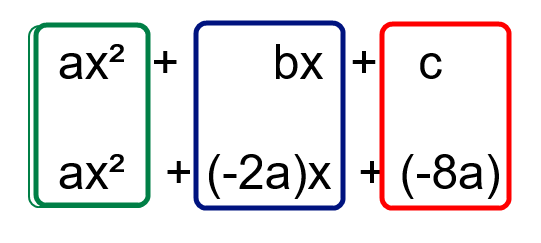Inscription / Connexion Nouveau Sujet
retrouver l'expression d'une fonction du second degré
Bonjour, je galère sur un DM depuis un bon moment, si quelqu'un peut m'aider je suis preneuse.
Soit une fonction f du second degré que l'on peut écrire sous la forme : ax2+bx+c
Sa courbe représentative est tracée ci-dessous :
parabole : (qui commence en -2 sur l'axe des abscisses, qui vient ensuite couper l'axe des ordonné en 16, et qui redescend en 4 sur l'axe des abscisse)
Questions :
1) déterminer la valeur de c
2) quelles sont les racines de f?
3) Donner la forme factorisée de f en fonction de a
4) développer-la et en déduire la valeur de a en identifiant les termes constants
5) déterminer la valeur de b (on pourra utiliser le sommet...)
6) donner l'expression de f(x)
J'ai repondu à la 1 : c'est 16
à la 2 : c'est -2 et 4
je suis donc bloquée à partir de la 3
merci d'avance
Bonjour
mets la figure s'il te plaît, ce sera plus simple pour suivre
extrait de 
la FAQ du forum :Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
modifie ton profil également (en allant dans espace membre), tu ne sembles plus être en seconde
extrait de la FAQ du forum :Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau sujet ?
équivalences des systèmes de niveaux scolairesBonjour,
C'est vrai qu'avec la figure, on y verrait plus clair.
Mais bon, on va essayer de faire sans 
3) La forme factorisée d'un polynôme du second degré ayant 2 racines x1 et x2 est :
ax²+bx+c = a(x-x1)(x-x2)
C'est du cours....
A toi de finir.
NB : "forme factorisée de f en fonction de a"
Je pense avoir retrouvé la courbe de ton énoncé....
Pour la question 4), tu n'as qu'à suivre strictement ce que l'énoncé te dit de faire :
* tu développes : tu trouves quoi ?
* quelle est dans cette forme développée en fonction de a, le terme constant c : c = ?
* tu identifies cette expression avec la valeur connue de c (voir question 1)..;
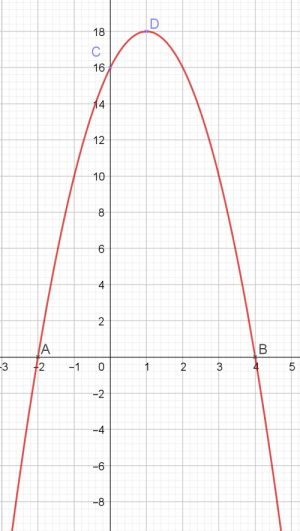
désolé, voici le graphique
j'ai donc trouvé : a(x+2)(x-4) pour la forme factorisée
sauf que pour la question suivante, en développant je tombe sur : ax2-2ax-8a, je pense que ce n'est pas ça car on recherche la valeur de a...
mon graphique ne s'est toujours pas publié mais votre parabole est exactement la même que la mienne !
je crois avoir trouvé ! à partir de a(x2-2x-8) j'ai utilisé delta ce qui m'a emmené sur 36, et je suis d'ailleurs retombée sur mes deux solutions x1 et x2 qui sont -2 et 4
Pouvez vous donc me confirmer si a=36?
je crois avoir trouvé ! à partir de a(x2-2x-8) j'ai utilisé delta ce qui m'a emmené sur 36, et je suis d'ailleurs retombée sur mes deux solutions x1 et x2 qui sont -2 et 4
Pouvez vous donc me confirmer si a=36?
Ta réponse est fausse. D'ailleurs la forme de la parabole (branches vers le bas) implique que "a" le coefficient de x² est NEGATIF.
Par ailleurs tu as écrit :
"en développant je tombe sur : ax²-2ax-8a", ce qui est exact. Dans cette forme développée quel est le terme constant ? (en fonction de a bien sûr)
Dans l'expression ax²-2ax-8a, ce que l'on appelle le terme constant c'est celui qui ne dépend pas de x...
Dans l'écriture ax²+bx+c, le terme constant c'est : c.
NB :
Ce nombre "c" est l'ordonnée du point B où la parabole coupe l'axe des ordonnées.
En effet si xB = 0 alors yB = a*0²+b*0+c = c
Tu cherches des choses compliquées alors que c'est... évident !
Dans l'expression
ax²-2ax-8a (qui est de la forme ax²+bx+c)
le terme de degré 2 est ax²
le terme de degré 1 est -2ax donc b= ??
et le terme constant est -8a donc c = ??
le terme de degré 1 est -2ax donc b= ??
et le terme constant est -8a donc c = ??
b est le coefficient de x donc b= -2a !
de même c = ??????
c=-8a
Je préfère cela
.
Donc on peut continuer.
L'énoncé dit :
4) [...] en déduire la valeur de a en identifiant les termes constants
Tu viens de trouver que l'expression du terme constant c est -8a.
Il doit donc y avoir quelque part une AUTRE expression de c !!
As tu déjà oublié la question 1 :
Questions :
1) déterminer la valeur de c
Tu a donné la bonne réponse qui est c = ????
(au fait comment as tu trouvé cette valeur de c ?)
Il ne te reste plus qu'a identifier ces 2 expressions... je te laisse faire (il n'y a pas de piège !)
vu que c=16 donc -8*?=16 sauf que -8*-2=16 donc a = -2
dans ma logique c'est ça après je pense que ma justification n'est clairement pas bonne... Comment justifier par les équations, je me suis embrouillée toute seule
Pour la question 1, j'ai déterminer graphiquement, je sais que dans mon équation c est l'ordonné à l'origine, l'ordonné à l'origine sur le graphique est 16
vu que c=16 donc -8*?=16 sauf que -8*-2=16 donc a = -2
Écriture un peu ... bizarre mais ta réponse est bonne !
Perso, j'aurais dit :
D'après la question 1) : c = 16
D'après la question 4) : c = -8a
donc -8a = 16
a = 16/(-8)
a= -2
Bon tu attaques la 5) ? c'est à nouveau une lecture graphique (voir l'aide de l'énoncé) !
A toi de faire et donc de trouver "b"
rebonjour, je n'avais pas vu votre réponse hier soir désolé...
En effet, c'est mieux comme ça !
Pour la 5), je n'arrive pas à savoir à quoi correspond b (comme par exemple c je sais que c'est l'ordonné a l'origine mais b?)
Ou alors b correspond tout simplement au sommet ?
Pour la 5), je n'arrive pas à savoir à quoi correspond b (comme par exemple c je sais que c'est l'ordonné a l'origine mais b?)
Ou alors b correspond tout simplement au sommet ?
Pas tout a fait aussi simple !
Tu as du voir ces notions en Seconde....
Revois ci dessous l'extrait d'une fiche de l'ïle aux maths...
Quelles sont les coordonnées du sommet de la parabole en fonction de a et b ?
Par lecture graphique, tu as constaté que :
les coordonnés du SOMMET de la parabole sont : (1;18)
Je t'avais demandé (en t'aidant de la fiche de cours jointe) :
Quelles sont les coordonnées du sommet de la parabole en fonction de a et b ?
Réponse (c'est dans la fiche de cours !!)
alpha = -b/2(a) et beta = f(alpha)
donc -b/(2a) = 1 => - b= 2a => b= -2a or a= -2 (question précédente) d'où :
b= +4 effectivement
excusez-moi, j'ai répondu trop vite
mais c'est exactement ce que j'ai fait sur papier libre pour trouver la valeur de b qui est donc de 4
je vous annonce que j'ai donc rendu mon DM aujourd'hui que j'ai pu finir hier soir. Je voulais vous remercier de votre patience, de votre gentillesse et de votre aide. Je n'aurai pas su le terminer sans vous. Merci encore, et bonne soirée
Annuler
connectez vous