Inscription / Connexion Nouveau Sujet
Rotation
Bon weekend à vous , j'ai besoin d'aide.
Merci d'avance.
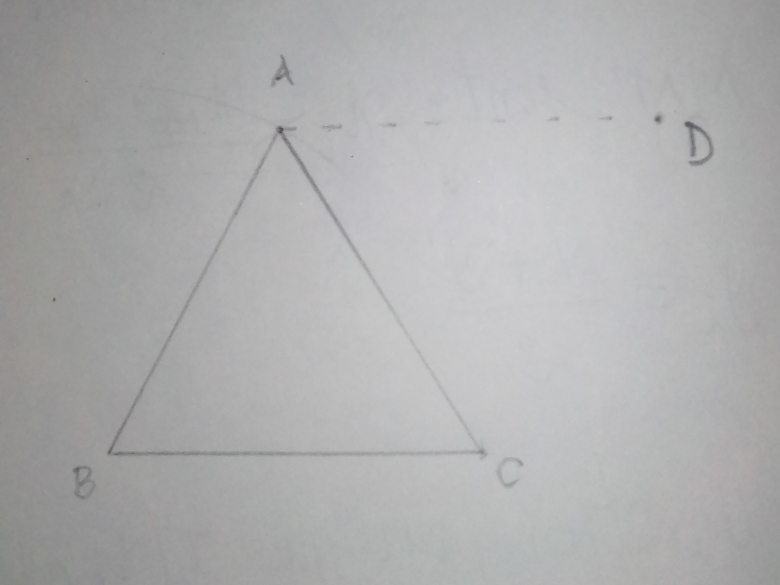
ABC est un triangle équilatéral de sens direct.
Soit r la rotation de centre A et d'angle , et r' la rotation de centre A et d'angle
.
1) Construire le point D image de B par r.
2) Justifier que : AB=AD et Mes
Réponses
1) Programme de construction.
Pour construire le point D image de B par r ,
Je fais une rotation du point B et de centre A tels que :
AB=AD et Mes
2)Je n'arrive pas à justifier que Mes puisque même l'image de B par r' n'implique pas que Mes
.
D'accord ,
Donc
1) Pour construire le point C image de B par r ,
Je fais une rotation du point B et de centre A tels que :
AB=AC et Mes
Et pour la 2e question ?
Oups
D'accord ,
Donc
1) Pour construire le point D image de C par r ,
Je fais une rotation du point B et de centre A tels que :
AC=AD et Mes
Et pour la 2e question ?
ben c'est toi qui a choisis l'exercice, donc tu le fais ! parce que là, à part avoir recopier un énoncé faux, tu n'as strictement rien fait !
tu ne vas pas te faire un recueil de nos solutions quand même...
Ben ... Du coup je n'ai plus de problème à cet exo parce que la seule chose que je ne pouvais pas faire était de justifier que Mes (AB,AD)=π/2
Et comme il s'agit d'une erreur d'énoncé ,
Après avoir corrigé la 1ere question , il suffit de corriger la 2e aussi :
2) L'image de B par r' est D.
Justifier que AB=AD et Mes(AB;AD)=π/6
J'aurais crû qu'il y avait quelque chose camouflée qui impliquait que Mes(AB,AD)=π/2 .
Bref ... Je me trompais.
Merci beaucoup
honnêtement, je ne comprends rien à ce que tu écris
Mes(AB;AD)=π/6 et en même temps Mes(AB,AD)=π/2
....
J'ai corrigé de sorte que je puisse faire l'exo , sinon comment démontrer que Mes(AB,AD)=π/2 ?
ABC est un triangle équilatéral de sens direct.
Soit r la rotation de centre A et d'angle
1) Construire le point C image de B par r.
2) L'image de B par r' est D.
Justifier que AB=AD et Mes(AB;AD)=π/6
Justifier que : AB=AD et Mes
bonjour
je pense à une erreur d'énoncé
1) Construire le point D image de C par r.
qui est la seule correction à faire dans ton sujet de départ.
Bien sûr, tu as fait une figure ...?
erreur de ma part, je n'ai pas vu qu'il manquait un' "prime"
1) Construire le point D image de C par r'
mais j'espère qu'il n'y a pas de question 3 qui risquerait de tout venir mettre en l'air
Non il n'y a pas de question 3 ,
je recopie et j'ai toujours recopié les énoncés entiers.
Voilà :
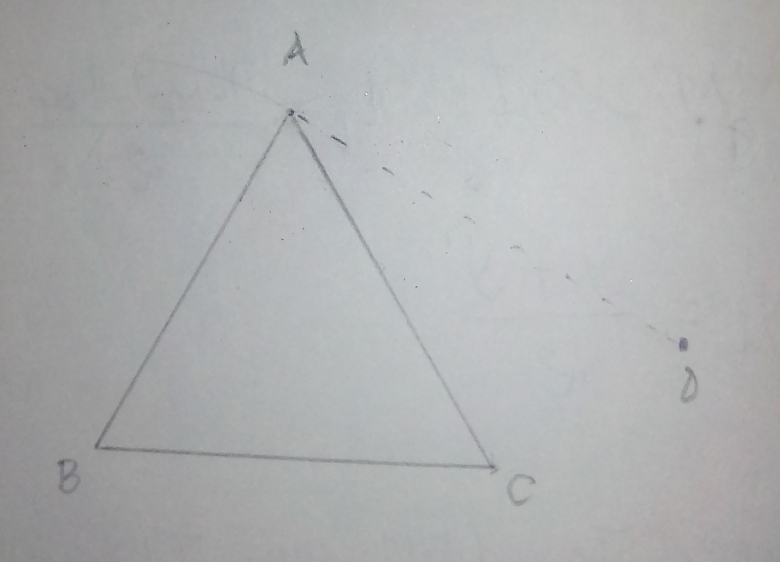
Mes (AB;AD)=π/2
pour qu'une construction soit valable (puisqu'il est dit "construire" c'est plus qu'une simple figure support de raisonnement) , elle doit être expliquée ou tout au moins tous les traits de construction indispensables doivent être laissés sur la figure.
Bonjour
[mode ironique on]
il ne peut y avoir aucun trait de construction ni de description d'un protocole de construction car pour Othnielnzue23 une construction de par exemple l'image de B par r (A; pi/3) c'est juste :
1) Pour construire le point C image de B par r ,
Je fais une rotation du point B et de centre A tels que :
AB=AC et Mes
[mode ironique off]
une construction c'est :
je trace un cercle de centre ... passant par ... un cercle de ... ... une droite passant par ... et le point d'intersection de ceci cela
etc
c'est ÇA une construction :
la façon explicite d'utiliser sa règle et son compas.
[mode critique on]
un énoncé qui commence par dire soit un triangle ABC équilatéral direct et qui demande de construire le point C, c'est loufoque à ce niveau
[all modes off]
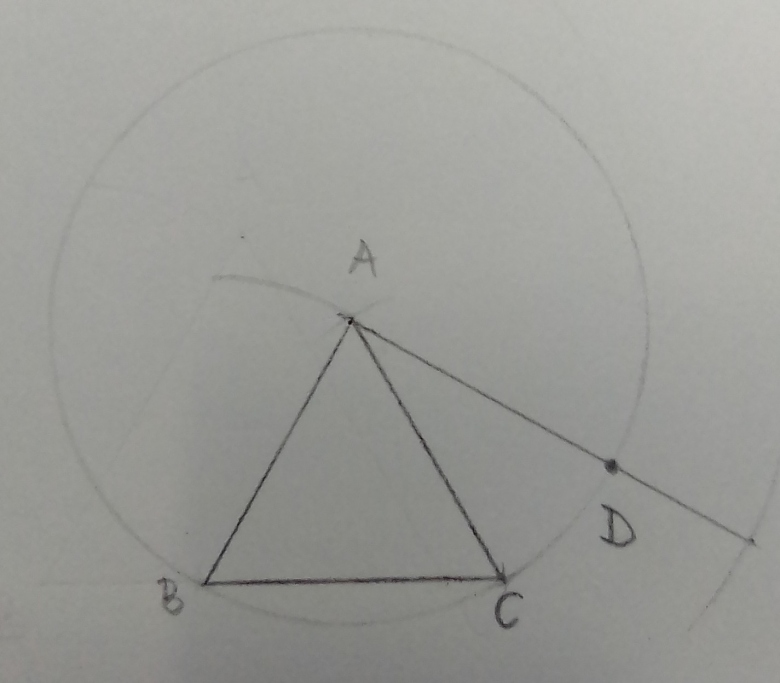
je trace un cercle (C) de centre A passant par les points B et C.
Le point D est tel Mes(AB,AC)=π/6
(le cercle (C) passe par les points B et C d'où passe forcément par D)
D'où D est le point d'intersection de la droite obtenu en construire Mes(AB,AC)=π/6 et le cercle (C).
admettons qu'on ne demande pas la construction du triangle ABC
je trace un cercle (C) de centre A passant par les points B et C. OK
Le point D est tel Mes(AB,AC)=π/6 pas de sens
(le cercle (C) passe par les points B et C d'où passe forcément par D) forcément n'est pas une construction
D'où D est le point d'intersection de la droite obtenu en construire quelle droite ? Mes(AB,AC)=π/6 et le cercle (C).
et pi/6, tu le construis au doigt mouillé ?
Je place A et B et je trace le segment [AB],je trace les cercles de centre A passant par B et de centre B passant par A, je construis C, un des points d'intersection des deux cercles, je termine en traçant les segments [BC] et [AC].
je trace un cercle (C) de centre A passant par les points B et C.
Le point D est tel Mes(AC,AD)=+π/6
D'où D est le point d'intersection de la droite(D) passant par le point A obtenu en construisant Mes(AC,AD)=+π/6 et le cercle (C).
.....je trace un cercle (C) de centre A passant par les points B et C avec le compas.
À l'aide du compas, je mesure la trajectoire du cercle (C) délimitée par les côtés [AC] et [AD]
Je place la pointe de mon compas sur le pont A. Je reporte 30° , je mesure sur la trajectoire A dans le sens de rotation demandé (anti-horaire)
Je nomme le nouveau point : D
oui, mais normalement comme toutes les constructions restent en plus de l'explication, ça "se voit"
donc je veux la construction de ce pi/6 (ou de ce point D, peu importe)
pourquoi ton point D est-il là ? pourquoi pas un peu plus haut sur le cercle ? un peu plus bas sur le cercle ?
je vois à droite en bas de l'image un arc de cercle concentrique au cercle passant par BCD, mais à quoi sert-il cet arc ?
bref...
construction de D toujours à faire correctement et à expliquer
je te signale que au moment de la construction de la figure, tu n'as pas encore justifié que cet angle valait pi/2 puisque c'est la question suivante
et si tu as fait ça, ce n'est pas avec un arc comme tu as fait sur ta figure qu'on dessine un angle de pi/2
tu dois savoir tracer des angles de pi/2 ; pi/4 ; pi/3 et pi/6 et ceux qui peuvent se déduire de ceux là
Waouh super , merci malou
Programme de construction
Je place A et B et je trace le segment [AB],je trace les cercles de centre A passant par B et de centre B passant par A, je construis C, un des points d'intersection des deux cercles, je termine en traçant les segments [BC] et [AC]: ( pour le triangle équilatéral ABC )
Ensuite je trace un cercle (C) de centre A passant par les points B et C.
Soit M un point tel que :
et AC=AM ,(C) passant par M.
On considère le quart de cercle avec AC et AM.
Les points E et F milieux respectifs des segments [AM] et [AC] .
Je trace la parallèle (D1) à (AC) passant par E et la parallèle (D2 à (AM) passant par F.
(D1) et (D2) coupent le cercle (quart de cercle avec AC et AM) en deux points Q et D tels que :
et
.
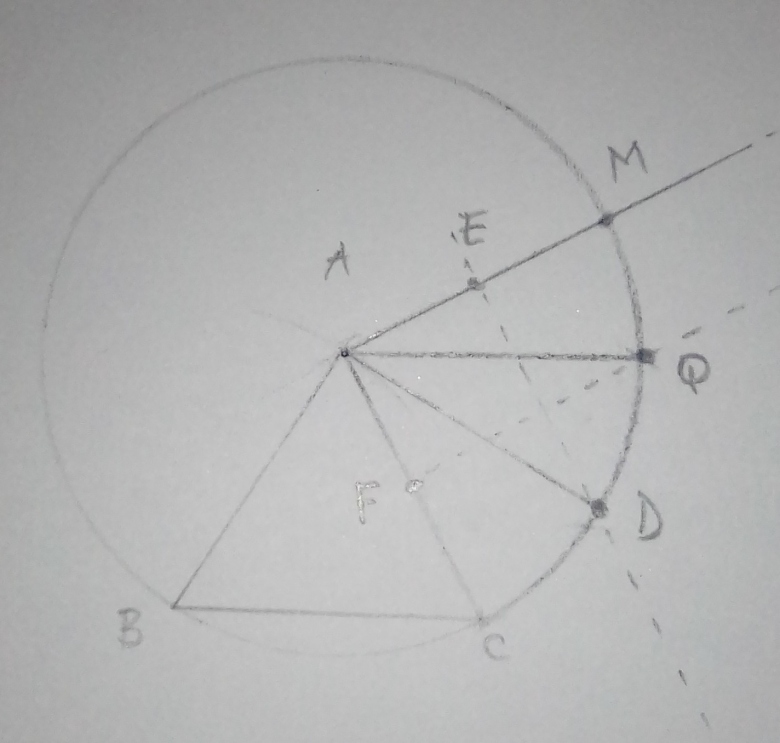
2) r et r' sont deux rotations de centre A et d'angles respectifs et
.
==> AB=AD et
Mes.
Merci beaucoup.
bonjour
la construction est complètement folklorique, tu n'as pas tiré profit du lien que je t'ai envoyé, entraîne toi en refaisant ce qu'on te montre sur ce fichier, pour ensuite savoir le faire dans n'importe quel cas de figure
2) ceci n'est pas une rédaction
je ne vois pas comment tu peux écrire ces enchaînements
on attend une rédaction en Français, avec des interruptions si nécessaires lorsqu'il y a un calcul à faire, c'est ça une rédaction
la construction est complètement folklorique
surtout inutilement compliquée !!!
on sait tracer un triangle équilatéral en deux coups de compas : ABC, d'accord
(il faut préciser que on choisit celui des deux points d'intersection qui donne un triangle direct)
pour construire ensuite l'angle de 30°, on construit au plus simple la bissectrice d'un angle de 60°, (cf doc de malou) c'est à dire d'un triangle équilatéral
par exemple de ton ACQ qui se construit par un seul coup de compas supplémentaire !! sans parallèles ni perpendiculaires inutiles !
et on termine par les deux coups de compas pour la bissectrice (cours de collège, ce tracé de bissectrice, voir doc citée par malou)
D'accord
2) r et r' sont deux rotations de centre A et d'angles respectifs et
r'(C)=r(A;π/6)=D et r(C)=r(A;π/3)=Q
D'où
==> AB=AD et
Mes
Q ne sert absolument à rien du tout dans la question 2 !!!
c'est juste un point intermédiaire pour la construction question 1 et rien d'autre.
je te parlais de la construction question 1 et de rien d'autre , suite à la remarque de malou "la construction est complètement folklorique"
question 2 :
r'(C)=r(A;π/6)=D FAUX
r(A;π/6) est une rotation (une transformation du plan tout entier) , pas le point D !!
dans tout ce que tu dis l'idée générale est bien là : composition deux rotations
(en jetant Q à la poubelle, iln'a roe à faore là dedans)
mais ce n'est toujours pas une rédaction valable.
(concepts en vrac, points choisis au hasard, enchaînement logique du raisonnement nébuleux pour ne pas dire absent)
2) r et r' sont deux rotations de centre A d'angles respectifs et
.
C est l'image de B par la rotation r: (car ABC est un triangle équilatéral direct) et
D est l'image de C par la rotation r' :
==> D est l'image de B par la composée r' o r de centre A et d'angle
:
==> AB=AD et Mes
c'est mieux, mais je ne l'écrirais pas comme ça
r et r' sont deux rotations de centre A d'angles respectifs et
.
donc r'or est une rotation de centre A.
Or .
donc r'or est la rotation de centre A et d'angle
r(B)=C car....(tu justifies avec l'énoncé)
r'or(B)=r'[r(B)]=r'(C) =D car ....(idem)
donc AB=AD et
fin
bonjour, une petite remarque :
on ne sait que r' o r est une rotation que une fois qu'on a calculé que la somme des angles n'est pas 0 [2pi]
car sinon ce serait une translation ou l'identité,
r et r' sont deux rotations d'angles respectifs ...
la somme de ces angles est ... et est différente de 0 [2pi], donc r' o r est une rotation
r et r' ont même centre A, ce point est donc invariant dans r' o r
donc r' o r est la rotation etc