Bonjour, j'ai besoin d'aide.

Merci d'avance.

ABC est un triangle de sens direct.

On construit à l'extérieur du triangle ABC les carrés ACRS ,BAMN puis le parallélogramme MASD dont on notera le centre I.

Le but de l'exercice est de démontrer que la droite (AD) est une hauteur du triangle ABC et que AD=BC.

On considère la rotation r de centre A , d'angle π/2.


1) Déterminer les images des points M et C par r.


2) On note S' l'image de S par r.

Démontrer que A est le milieu de [CS'].

3) On note I' l'image de I par r.

Démontrer que I' est le milieu de [BS'] .

4) En déduire que (AD) est perpendiculaire à (BC) et que AD=BC.

J'ai pu faire le schéma de la situation avec GeoGebra.



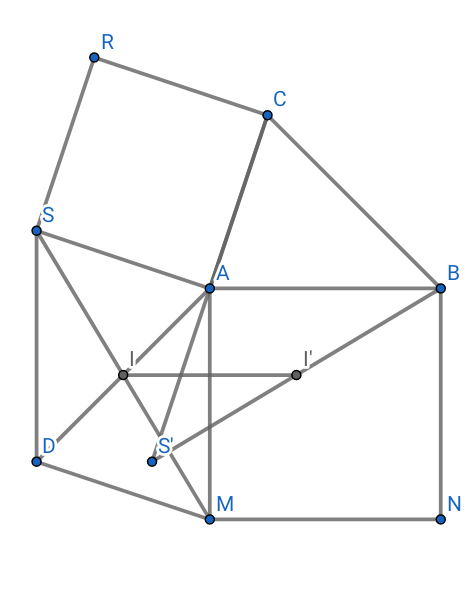
Réponse


1) r(M)=B (car Mes(AM;MB)=π/2 ) et r(C)= S (car Mes( AC;AS)=π/2)

2)on a r(C)=S et r(S)=S'

r(C) o r(S) est la composée de deux rotation de même centre :A et de même angle :π/2.

==>
R(C) o r(S)=r(A;π)=S_A

==> r(C) o r(S)(C)=S_A(C)=S'

==> A est le milieu de [CS']

3) on a r(M)=B et r(C)=S

r(M) o r(C)  est la composée de deux rotations de même centre:A et de même angle:π/2

==> r(M) o r(C)=r(A;π)=S_A

==> r(M) o r(C)(B)=S_A(B)=S'

Donc A est le milieu de [BS'].

4)Considérons le triangle BCS'.

A est le milieu de [ CS'] et I' le milieu de [BS']

D'après le théorème de la droite des milieux , (BC)//(AI') et .

Or r(A;π/2)(I)=I' donc r(A;-π/2)(I')=I
==> (AI) (BC)

==> (AD) (BC).


I milieu du parallélogramme MASD d'où I milieu de [AD] , I' est son image par r donc IA=I'A

==> AD=2IA=2I'A et BC=2I'A

==> AD=2I'A et BC=2I'A