Inscription / Connexion Nouveau Sujet
rotation et angles
Bonjour
on nous donne un triangle ABD tel que (vect BA;vect BD)
 /6[2
/6[2 ]
]
on note S(AB) et S(BD) les symétries orthogonales
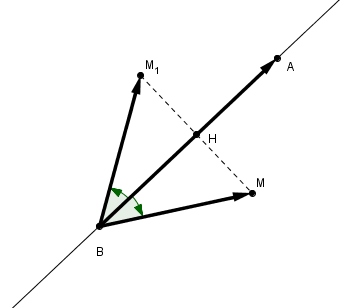
1) soit un point M différent de B .
a) construire l'image M1 de M par S(AB) et l'image M2 de M1 par S(BD).
b) comparer BM et BM2 et déterminer l'angle (vect(BM);vect(BM2)).
2) en déduire la nature de l'application du plan qui transforme M en M2.
j'ai trouver BM=BM2 mais j'ai pas su comment trouver l'angle
Merci de vouloir m'aider.
Bonsoir,
1) b) Soit N1 le point d'intersection de la droite (M1M) avec la droite (BA) qui sont perpendiculaires l'une de l'autre
On sait puisque M1 est le symétrique de M que M1N1 = N1M et donc avec Pythagore que BM1 = BM
On sait aussi que l'angle (BM1,BM) est le double de l'angle (BM,BA)
On fait le même raisonnement pour le point M2
On trouve donc que BM2=BM1 et que l'angle (BM1,BM2) est le double de l'angle (BM1,BD)
On en déduit donc que BM2 = BM et que l'angle (BM2,BM) est le double de l'angle (BA,BD)
2) Il s'agit d'une rotation de  /3
/3
bonjour,
faire un dessin ?
sinon, de façon plus "en ligne" avec un exo sur les angles orientés :
il est facile (dessin) de montrer que la symétrie par rapport à (AB) est équivalente à
||BM1|| = ||BM|| (fait) et
on calcule alors par Chasles
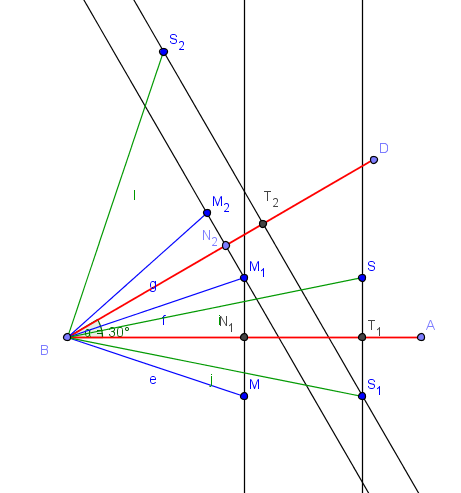
J'ai fait avec Geogebra le schema avec les 2 cas
le point M n'est pas entre les droites (BA) et (BD)
le point M (appelé S pour le distinguer du précédent) est entre les droites (BA) et (BD)
Cela devrait t'aider
l'avantage d'utiliser dès le départ et dans tout le calcul des angles orientés est qu'il n'y a qu'un seul cas ...
(c'est valable sans se poser de question quel que soit M partout dans le plan sauf en B car alors les vecteurs sont nuls)