Inscription / Connexion Nouveau Sujet
Savoir si une fonction est dérivable à partir de la courbe
Bonjour,
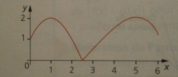
dans un exercice on me dit que f est la fonction définie sur [0;6] dont on peut voir la courbe.
On me demande de choisir entre 3 reponses (QCM):
1)Au point d'abscisse 1:
a) f n'est pas dérivable b)f est derivable et f'(1)=0
c)f est dérivable et f'(1)=-1.
Comment savoir si f est dérivable en sachant que je n'ai pas la fonction mais seulement la courbe ?
Merci d'avance
Bonjour,
une fonction n'est pas dérivable en un point :
- si au point en question la tangente est verticale (auquel cas la dérivée serait infinie et la fonction ne serait pas dérivable)
- s'il y a une rupture de pente, un point anguleux. c.a.d si la dérivée à gauche n'est pas égale à la dérivée à droite.
- si la fonction n'est pas continue (fait un saut au point en question).
Si tu n'es pas dans un de ces cas là et que la tangente à la courbe au point en question est une droite normale (non verticale), alors la fonction est dérivable (et vaut le coefficient directeur de la tangente).
Ben si il y a une tangente, il faut l'imaginer si elle n'est pas dessinée.
Au point d'abscisse 1 par exemple il n'y a pas de problème
Au point d'abscisse 2.5 par contre il y en aurait un, il y a une rupture de pente et la fonction n'est pas dérivable en ce point.
Ben non, au point 1, la tangente est horizontale, donc de pente nulle donc f '(1)=0
(c'est f(1) qui est égal à 2, ne confond pas la fonction et sa dérivée).
ni horizontale. D'ailleurs si tu estimes que f '(4)=1 c'est qu'elle fait plutôt un angle de 45°.
tu sais vraiment ce que veux dire vertical et horizontal ? on dirait pas.
Ben elle l'est, si la tangente existe et n'est pas verticale, la fonction est dérivable. Relie les conditions dans mon premier post.